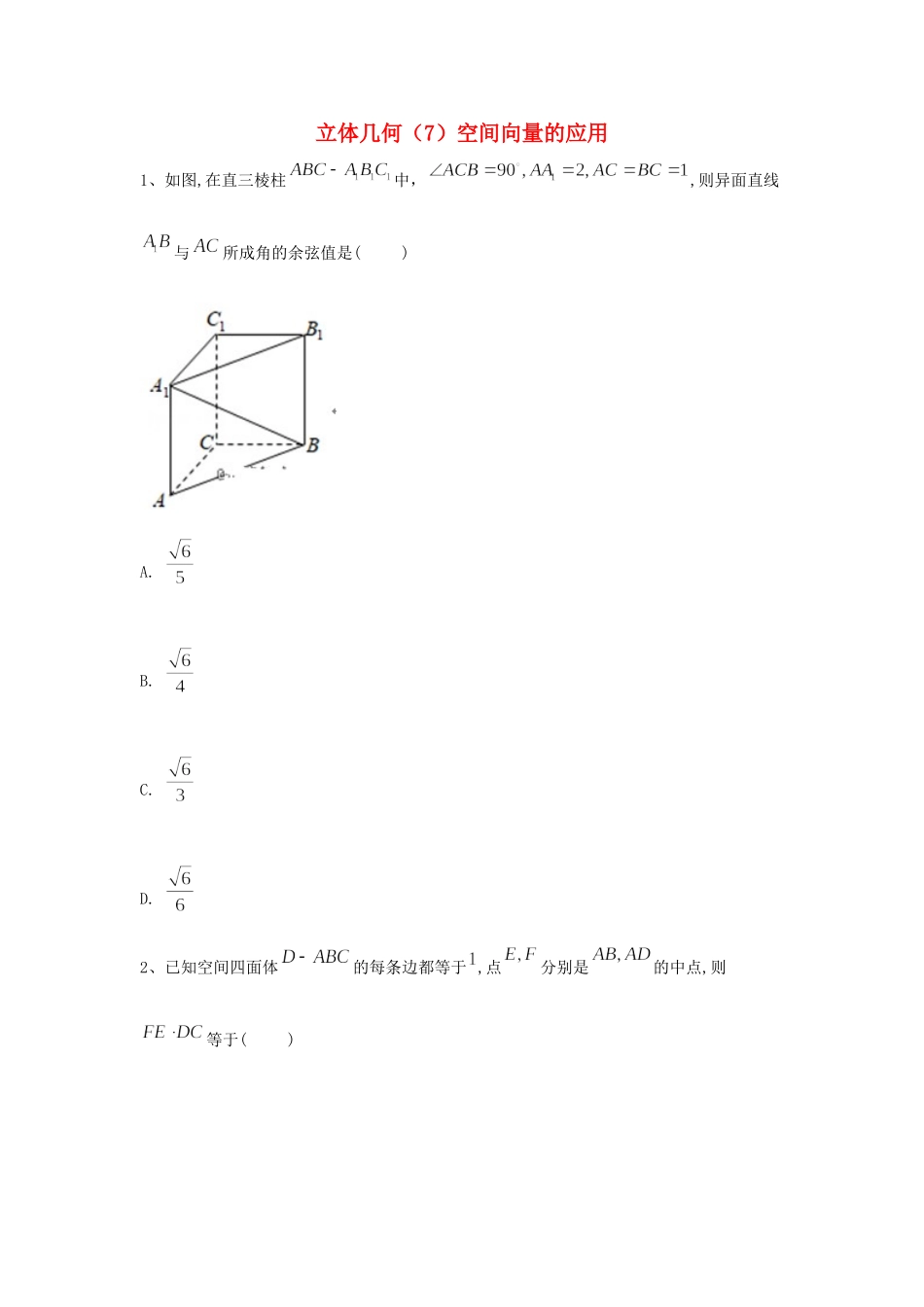
立体几何(7)空间向量的应用1、如图,在直三棱柱中,,则异面直线与所成角的余弦值是()A.B.C.D.2、已知空间四面体的每条边都等于,点分别是的中点,则等于()A.B.C.D.3、我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点,且法向量为的直线(点法式)方程为,化简得类比以上方法,在空间直角坐标系中,经过点,且法向量为的平面的方程为()A.B.C.D.4、已知,则平面的单位法向量为()A.B.C.D.5、已知正方体中,分别为的中点,那么直线与所成角的余弦值为()A.B.C.D.6、在正三棱锥中,在棱上,在棱上,且为异面直线与所成的角,为异面直线与所成的角,则的值是()A.B.C.D.7、如图,四棱锥中,底面,底面是直角梯形,是侧棱上靠近点的四等分点,.该四棱锥的俯视图如图所示,则的大小是()A.B.C.D.8、若平面的一个法向量为,平面的一个法向量是,则平面与所成的角等于()A.B.C.D.9、已知球的半径为,四点均在球的表面上,且,则点到平面的距离为()A.B.C.D.10、两平行平面分别经过坐标原点和点且两平面的一个法向量,则两平面间的距离是()A.B.C.D.11、已知直线的方向向量为,平面的法向量为,且,则__________12、已知长方体内接于球,底面是边长为2的正方形,为的中点,平面,则球的表面积为__________.13、如图,在四棱锥中,平面,底面为直角梯形,,且分别为线段上的一点(端点除外),满,则当实数的值为__________时,为直角.14、已知平面的一个法向量为,其中,,则点到平面的距离为__________.15、如图,在四棱锥中,,且.1.证明:平面平面;2.若,,求二面角的余弦值.答案以及解析1答案及解析:答案:D解析:2答案及解析:答案:A解析:3答案及解析:答案:C解析:类比得:即故选C.4答案及解析:答案:D解析:设平面的一个法向量为,则且,即,且,即解得,∴,故平面的单位法向量.故选D.5答案及解析:答案:B解析:6答案及解析:答案:D解析:当时,,从而,此时是是与所成的角,因此,排除A,B,C.故选D.7答案及解析:答案:C解析:8答案及解析:答案:D解析:9答案及解析:答案:B解析:10答案及解析:答案:B解析:11答案及解析:答案:-8解析:12答案及解析:答案:解析:∵长方体内接于球,底面ABCD是边长为2的正方形,设,E为的中点,以A为坐标原点,分别以AB、AD、为x、y、z轴建立空间直角坐标系,∴,,,,,,∴,,,若平面BDE,∴,即,即,解得,∴球的半径R满足:,∴球的表面积.考点:球的体积和表面积.13答案及解析:答案:解析:因为平面,故可建立如图所示的空间直角坐标系.因为,所以.设,则,因为,所以,所以,所以.同理,,所以.要使,则,又所以,所以,所以.14答案及解析:答案:解析:15答案及解析:答案:1.∵,∴,,∵,∴,∵,且,平面,∴平面,∵平面,∴平面平面.2.取中点为,∵,∴为等腰三角形,∴,∴,.取中点,连接,则,∴,∵平面,∴平面,∴,∴,,两两互相垂直.以为坐标原点,以为轴,为轴,为轴建立空间直角坐标系,如图:∴,设,∴,,,∴,,,设平面的法向量为,平面的法向量为,则∴∴,,∴.显然二面角为钝角,所以它的余弦值为.解析: