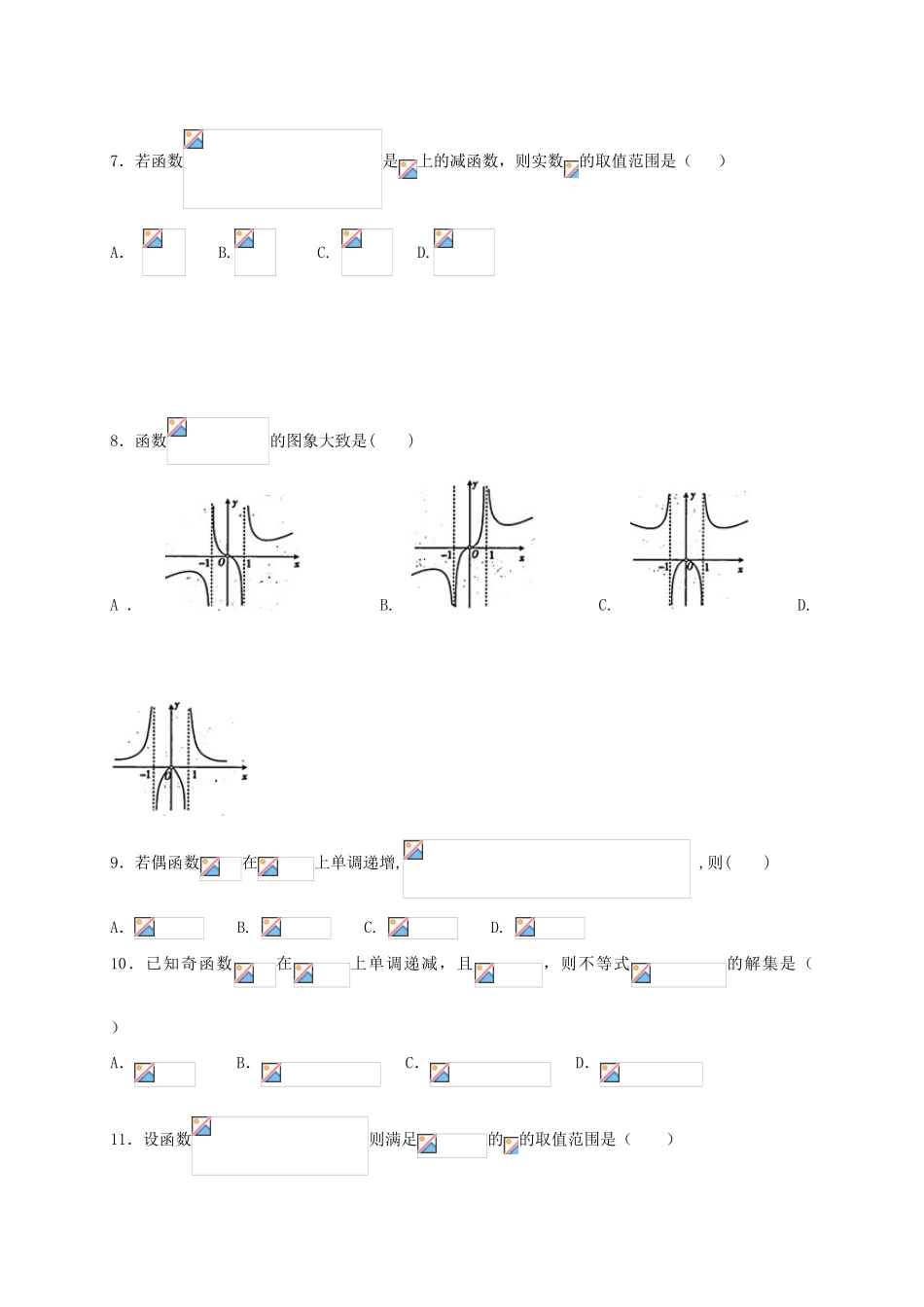
湖北省宜昌市2017-2018学年高一数学上学期期中试题考试时间:120分钟一、选择题:本大题共12小题,每小题5分,共60分1.已知集合,则=A.B.C.D.2.下列各组函数中,表示同一函数的是()A.x与B.与C.与D.与3.已知函数(且)的图象恒过定点,则点的坐标是()A.B.C.D.4.函数的定义域为()A.B.C.D.5.已知函数的对应关系如下表,函数的图象是如图的曲线,其中,,,则的值为()A.3B.0C.1D.26.已知函数,则=()A.30B.19C.6D.207.若函数是上的减函数,则实数的取值范围是()A.B.C.D.8.函数的图象大致是()A.B.C.D.9.若偶函数在上单调递增,,则()A.B.C.D.10.已知奇函数在上单调递减,且,则不等式的解集是()A.B.C.D.11.设函数则满足的的取值范围是()A.B.C.D.12.设函数,若关于的方程有四个不同的解,且,则的取值范围是()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分13.若函数的定义域为,值域为.14.已知且,则=.15.函数单调递减区间是.16.已知函数,若方程有3个不等的实根,则实数的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤17.(10分)(1)计算(2)计算;18.(12分)已知集合,.(1)当时,求,;(2)若,求实数的取值范围.19.(12分)已知函数,(1)若在上单调递减,求的取值范围;(2)求在上的最小值.20.(12分)已知满足(1)求的取值范围;(2)求函数的值域.21.(12分)设函数.(1)判断函数的奇偶性;(2)探究函数,上的单调性,并用单调性的定义证明.22.(12分)设是实数,,(1)若函数为奇函数,求的值;(2)若函数为奇函数,且不等式对任意恒成立,求实数的取值范围。参考答案1-12.BCABD,BCACD,AD【解析】作出函数和的图象(如图所示),若关于的方程有四个不同的解且,则且,即,且,则在区间上单调递增,则,即的取值范围为;故选D.二、填空题13.(-5,+)14.-25,15.16.(0,2)【解析】画出函数图像如图所示,得二次函数最高点位,常函数和曲线有三个交点,则位于轴上方,最高点下方即可.故得.17.(1(2)18.(1);(2).(1)当时,,又,所以.因为所以.(2)由得,于是或,解得或.故实数的取值范围是·19.(1);(2)(1)的对称轴是又在上单调递减(2)的对称轴为当,即时,,当,即时,20.解:(1)因为由于指数函数在上单调递增(2)由(1)得令,则,其中因为函数开口向上,且对称轴为函数在上单调递增的最大值为,最小值为函数的值域为.21.(1)的定义域,为奇函数;(2)函数在上的单调递增,证明:,,任取,且则,且,,,则,即函数在上的单调递增.22.(1)(2)详见解析(3)试题解析:(1)∵,且∴(注:通过求也同样给分)∴(2)证明:设,则∵∴∴即。所以在R上为增函数。(3)因为为奇函数且在R上为增函数,由得:∴即对任意恒成立。令问题等价于对任意恒成立。令,其对称轴当即时,,符合题意。当时,即时,对任意,恒成立,等价于解得:综上所述,当时,不等式对任意恒成立