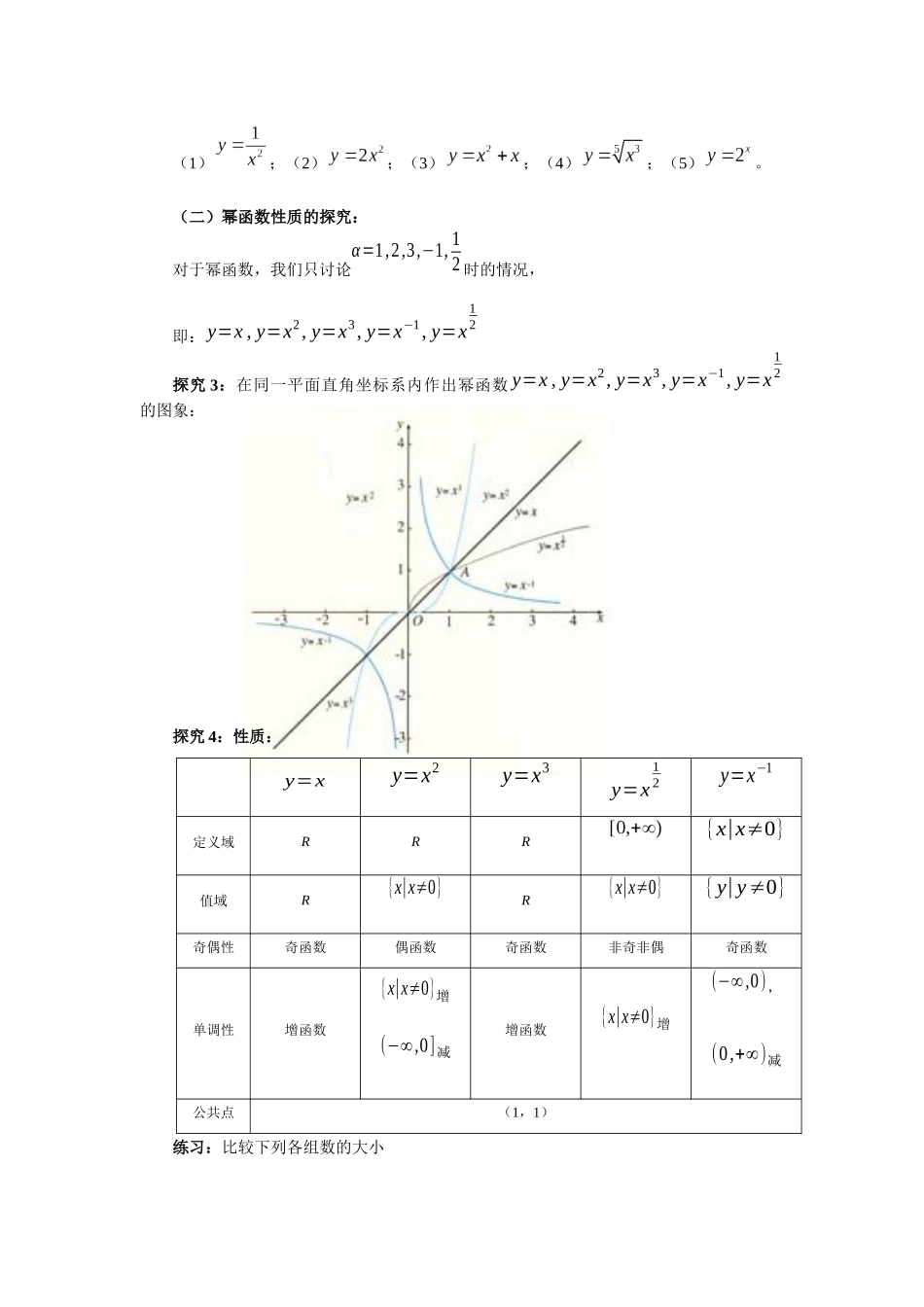
2.3幂函数三维目标定向〖知识与技能〗(1)了解幂函数的概念;(2)会画函数y=x,y=x2,y=x3,y=x−1,y=x12的图象,并了解它们的变化情况。〖过程与方法〗通过画y=x,y=x2,y=x3,y=x−1,y=x12的图象,由特殊到一般,归纳出幂函数的图象和性质。〖情感、态度与价值观〗通过大量实例,感受幂函数的概念,体会幂函数在客观现实中的应用,学会应用数学的方法,形成一定的数学应用意识。教学重难点:幂函数的图象和性质。教学过程设计一、实例剖析引例:(1)如果张红购买了每千克1元的蔬菜x千克,那么她需要支付y=元;(2)如果正方形的边长为x,那么正方形的面积y=;(3)如果立方体的边长为x,那么立方体的体积y=;(4)如果一个正方形场地的面积为x,那么这个正方形的边长为y=;(5)如果某人xs内骑车行进了1km,那么他骑车的平均速度y=km/s。问题:以上函数具有什么共同特征?共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。二、幂函数的图象和性质(一)定义:函数y=xα叫做幂函数。(其中x为自变量,α为常数)探究1:你能说出幂函数与指数函数的区别吗?式子名称axy指数函数:底数指数幂值幂函数:指数底数幂值探究2:如何判断一个函数是幂函数还是指数函数?看看自变量x是指数(指数函数)还是底数(幂函数)。练习:1、下面几个函数中,哪几个函数是幂函数?(1);(2);(3);(4);(5)。(二)幂函数性质的探究:对于幂函数,我们只讨论α=1,2,3,−1,12时的情况,即:y=x,y=x2,y=x3,y=x−1,y=x12探究3:在同一平面直角坐标系内作出幂函数y=x,y=x2,y=x3,y=x−1,y=x12的图象:探究4:性质:y=xy=x2y=x3y=x12y=x−1定义域RRR{x|x≠0}值域R{x|x≠0}R{x|x≠0}{y|y≠0}奇偶性奇函数偶函数奇函数非奇非偶奇函数单调性增函数{x|x≠0}增(−∞,0]减增函数{x|x≠0}增(−∞,0),(0,+∞)减公共点(1,1)练习:比较下列各组数的大小(1)32,42(2)(-3)2,(-4)2(3)(-3)3,(-4)3(4)312,412(5)(-3)-1,(-4)-12、已知幂函数y=f(x)的图象经过点(3,),求这个函数的解析式。3、如果函数是幂函数,求实数m的值。三、思考题证明幂函数f(x)=√x在{x|x≠0}上是增函数。