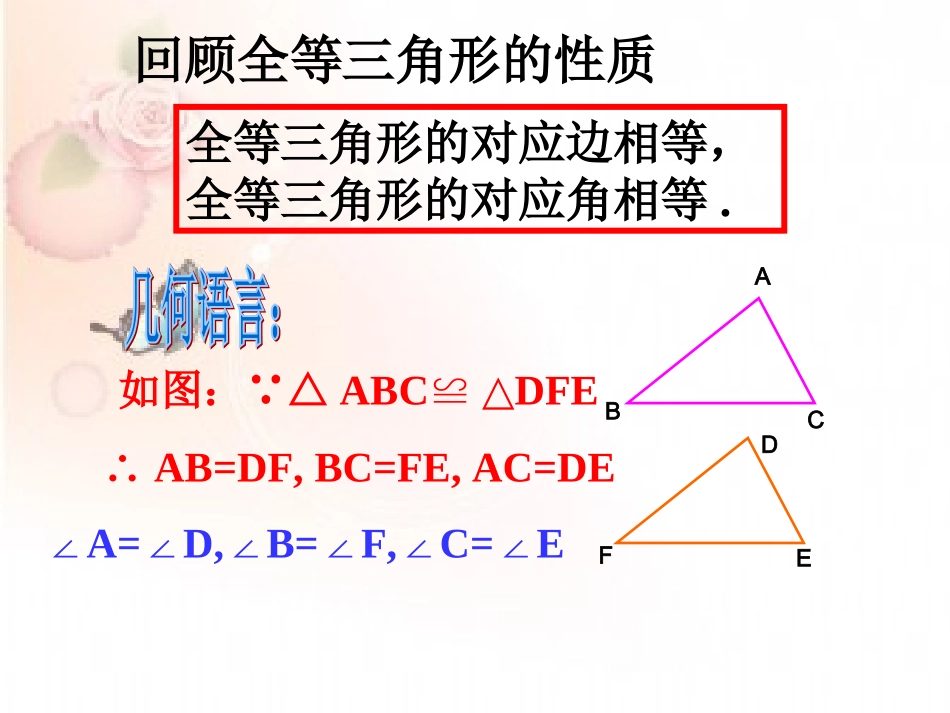
11.2全等三角形的判定全等三角形的对应边相等,全等三角形的对应角相等.如图: △ABC≌DFE△∴AB=DF,BC=FE,AC=DE∠A=D,B=F,C=E∠∠∠∠∠DEFABC回顾全等三角形的性质一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一个与原来同样大小的新教具吗?怎样才能保证制作的新教具与原来的全等呢?怎么办?怎么办?可以帮帮可以帮帮我吗?我吗?新课导入新课导入新课导入新课导入CBEAD11.一个条件..一个条件.((11)有一条边对应相等的三角形?)有一条边对应相等的三角形?不一定不一定全等.全等.三角形全等的探究三角形全等的探究判断两个三角形全等的推理过程,叫做证明三角形全等.((22)有一个角对应相等的三角形?)有一个角对应相等的三角形?一个条件,并不能保证三一个条件,并不能保证三角形全等.角形全等.不一定不一定全等.全等.结论结论结论结论不一定不一定全等.全等.((11)三角形的一个角和一条边对应)三角形的一个角和一条边对应相等的三角形?相等的三角形?22.两个条件..两个条件.((22)三角形的两条边对应相等的)三角形的两条边对应相等的三角形.三角形.不一定不一定全等.全等.有两个条件对应相等也不有两个条件对应相等也不能保证三角形全等.能保证三角形全等.结论结论结论结论已知△ABC,画一个△DEF,使DE=AB,EF=BC,DF=AC.1.画线段DE=AB;2.分别以D、E为圆心,线段AC、BC为半径画弧,两弧交于点F;3.连接线段DF、EF.DEABCF((11)三角形的三条边分别)三角形的三条边分别对应相等的三角形?对应相等的三角形?33.三个条件..三个条件.知识要点知识要点知识要点知识要点三角形全等的条件:三角形全等的条件:三边分别相等的两个三角形全等三边分别相等的两个三角形全等..简写:“边边边”或“简写:“边边边”或“SSS”SSS”AB=A’B’AB=A’B’BC=B’C’BC=B’C’AC=A’C’AC=A’C’((SSSSSS))ABCA′B′C′在△在△ABCABC和△和△A’B’C’A’B’C’中中∴△∴△ABCA’B’C’≌△ABCA’B’C’≌△用几何语言表达为:用几何语言表达为:ABCD例1已知△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABDACD.≌△证明: 点D是BC的中点,∴BD=CD.证明: 点D是BC的中点,∴BD=CD.在△ABD和△ACD中,AB=AC,AD=AD(公共边),BD=CD,∴△ABDACD≌△(SSS).在△ABD和△ACD中,AB=AC,AD=AD(公共边),BD=CD,∴△ABDACD≌△(SSS).在△ABC中,AB=AC,D是BC中点,点E在AD上.找出图中全等的三角形,并说明它们为什么是全等的?(课本45页13题)D想一想想一想想一想想一想BCAE1.已知:如图,AB=AD,CB=CD.求证:∠B=D∠.在△ABC和△ADC中,∴△ABCADC≌△(SSS).∴∠B=D∠(全等三角形的对应角相等).证明:连结AC,BCDAAB=AD,CB=CD,AC=AC(公共边),练一练一练练练一练一练练证明: BE=CF(已知),即BC=EF.在△ABC和△DEF中,AB=DE(已知),AC=DF(已知),BC=EF(已证),∴△ABCDEF≌△(SSS).∴∠A=D∠(全等三角形对应角相等).FABECD∴BE+EC=CF+EC,2.如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=D∠.(课本44页第9题)1.了解三角形的稳定性;2.掌握三角形全等的条件:边边边(sss)3.能运用全等三角形的条件,解决简单的推理证明问题.谈谈自己的收获谈谈自己的收获回顾总结回顾总结回顾总结回顾总结((22)三角形的两条边和它们的夹)三角形的两条边和它们的夹角对应相等的三角形角对应相等的三角形??已知△ABC,画一个△A'B'C',使A'B'=AB,B'C'=BC,∠B'=B∠.ABC1.画∠B’=B∠;2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.3.连接A’C’.以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O于点P;以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;过点Q画射线B’F,则∠OB’F=B∠ABCA’B’C’MNOPQF··知识要知识要点点知识要知识要点点““边角边”或“边角边”或“SAS”SAS”两边和它们的夹角对应相等的两个两边和它们的夹角对应相等...