2412垂直于弦的直径(第2课时)VIP免费

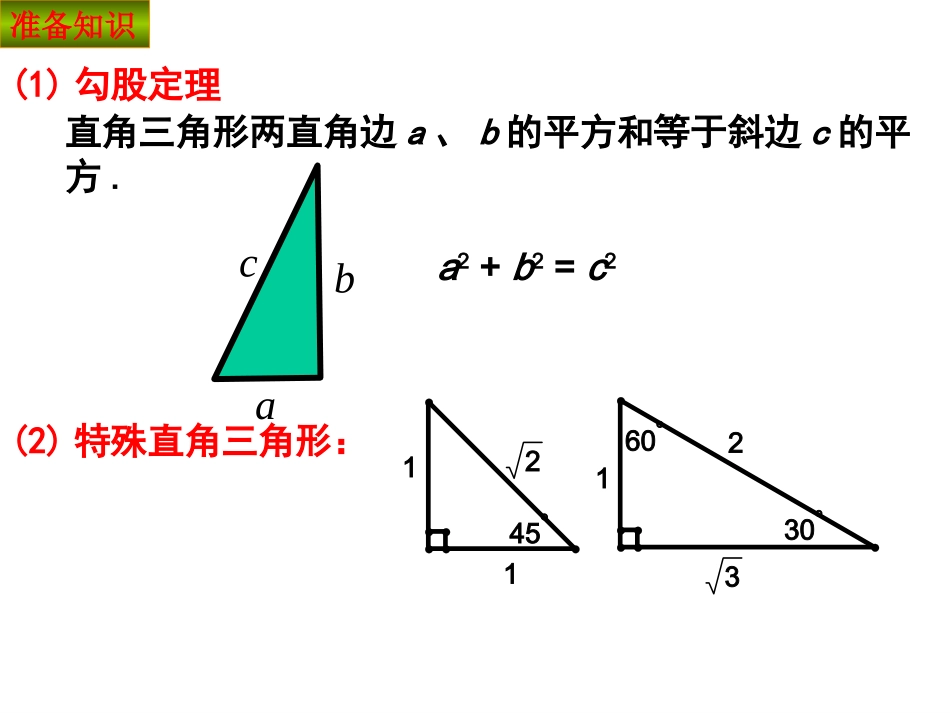
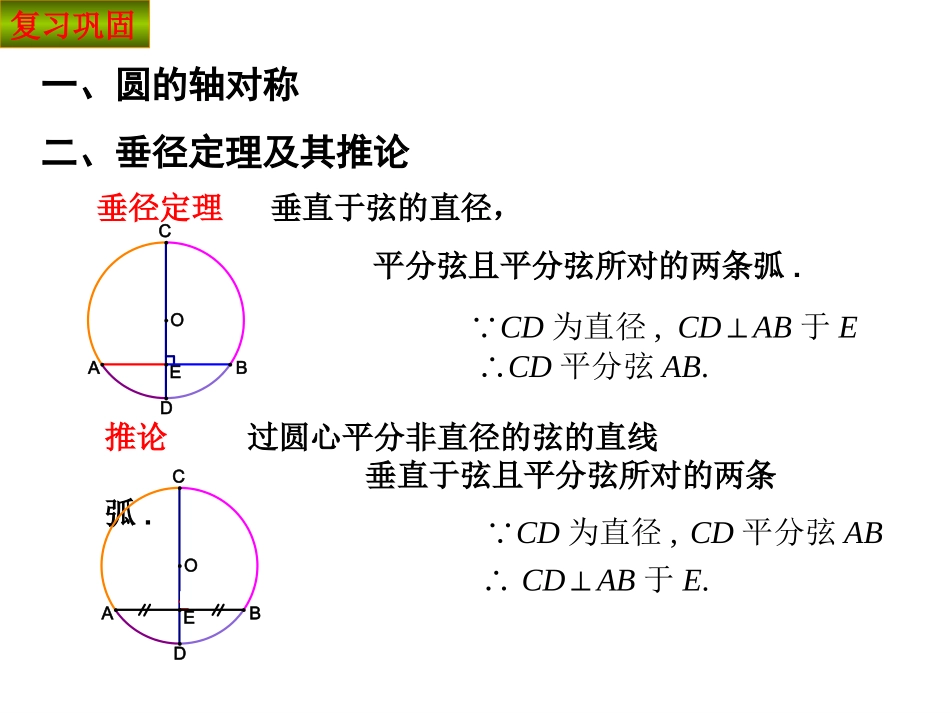
第二十四章圆24.1.224.1.2垂直于弦的直径垂直于弦的直径（第（第22课时）课时）北京市东方德才学校张艳伶24.124.1圆圆322111603045直角三角形两直角边a、b的平方和等于斜边c的平方.a2+b2=c2(1)勾股定理准备知识abc(2)特殊直角三角形：一、圆的轴对称二、垂径定理及其推论复习巩固垂径定理垂直于弦的直径，平分弦且平分弦所对的两条弧.∵CD为直径,CD⊥AB于E∴CD平分弦AB.推论过圆心平分非直径的弦的直线垂直于弦且平分弦所对的两条弧.∵CD为直径,∴CD⊥AB于E.CD平分弦ABDCEABODCEABO如图，已知CD是⊙O的直径，AB⊥CD于E，CE=8cm,DE=2cm,则AB=.练习DCEABO8cm在圆中解决有关弦的问题时，作垂径，连半径，构造直角三角形.总结弦心距半径半弦弦心距2+半弦2=半径2AB.OE例题解析DCEABO例1.如图，⊙O的弦AB=8㎝，直径CD⊥AB于E，DE=2㎝，求半径OD的长.2.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=米.3.如图是圆弧形的蔬菜大棚的剖面,AB=8m,如果大棚的高度CD=2m,那么弧AB所在的圆的半径长为m．练习1.如图，⊙O的弦AB=6㎝，直径CD⊥AB于E，CE=9㎝，求半径OD的长.第1题第2题第3题DCEABO5cm5737例2赵州桥的主桥拱是圆弧形,它的跨度（弧所对的弦的长）为37.4米,拱高（弧中点到弦的距离）为7.2米,你能求出赵州桥主桥拱的半径吗？OAB37.4米7.2米18.7米7.2米RR-7.2例题解析解：如图，用表示桥拱，所在圆的圆心为O，半径为Rm，经过圆心O作弦AB的垂线OD，D为垂足，与相交于点C.根据垂径定理，D是AB的中点，C是的中点，CD就是拱高.由题设ABABABAB,2.7,4.37CDABABAD21,7.184.3721DCOCOD.2.7R在Rt△OAD中，由勾股定理，得,222ODADOA.)2.7(7.18222RR即解得R≈27.9（m）.答：赵州石拱桥的桥拱半径约为27.9m.OABCRD37.47.2生活中的应用●OABCDM└CD⊥AB,如图∵CD是直径,∴AM=BM,⌒⌒AC=BC,⌒⌒AD=BD.条件CD为直径CD⊥ABCD平分弧ADBCD平分弦ABCD平分弧AB结论复习巩固1.垂径定理相当于说一条直线如果具备(1)过圆心(直径);(2)垂直于弦;则它有以下性质(1)平分弦;(2)平分弦所对的劣弧;(3)平分弦所对的优弧.课堂小结这节课中，你有什么收获？课堂小结AB.OE2.在圆中解决有关弦的问题时,经常是作弦心距,连结半径等辅助线，为应用垂径定理创造条件.检测题1．如图，如果AB为⊙O的直径，CD⊥AB，垂足为E，那么下列结论中，错误的是（）A．CE=DEB．BC=BDC．∠BAC=∠BADD．AC>AD2．如图，AB为⊙O的直径，弦CDAB，垂足为点E，连接OC，若OC=5，AE=2，则CD等于（）A．3B．4C．6D．8OEDCBA（4题图）BACEDODD例题解析检测题3．如图，在直径为52cm的圆柱形油槽内，装入一些油后，截面如图所示，如果油的最大深度CD为16cm，那么油面宽度AB是多少？2．如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（）A.3≤OM≤5B.4≤OM≤5C.3＜OM＜5D.4＜OM＜5（提高题）3．如图，⊙O直径AB和弦CD相交于点E，AE=2，EB=6，∠DEB=30°，求弦CD长．BACEDO课后作业1.教科书P82练习第1、2题，P87第1题,P88第8、9题.第2题图第3题图