22向量的减法课件VIP免费

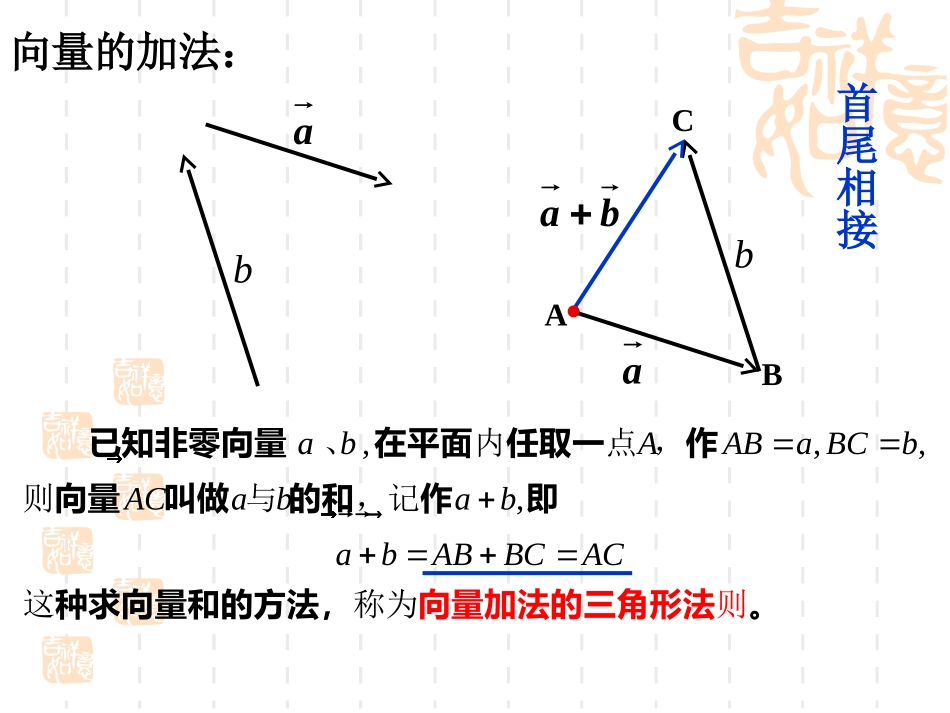
§2.2§2.2向量的减法向量的减法§2.2§2.2向量的减法向量的减法引入新课新知探究应用示例智能训练课堂小结作业向量的加法：abbaabCAB,,,,abAABaBCbACabababABBCAC�����、内点，则与，记则这称为已知非零向量在平面任取一作向量叫做的和作即种求向量和向量加法的三角方法，形法的。首尾相接向量的加法：OABCabba,OabOACBOOCaabbabOAOBOC���点为点两个为邻边则为点对线与这平行四边则称为,以同一起的已知向量、作以起的角就是的和即向量加法的种求向量和的方法，形法。起点相同向量加法的平行四边形法则和三角形法则的区别与联系三角形法则中的两个向量是首尾相接的，而平行四边形法则中的两个向量有公共的起点；三角形法则适用于所有的两个非零向量的求和，而平行四边形法则仅适用于不共线的两个向量的求和。三角形法则和平行四边法则虽然都是求向量和的基本方法。但在应用上也有讲究，求两个向量和，当一个向量的终点为另一个向量的始点时，可用向量加法的三角形法则；而当它们的始点相同时，可用向量加法的平行四边形法则。)cb(ac)ba(abba向量的加法与实数的加法类似，那么向量的减法运算呢？在数的运算中，我们知道减法是加法的逆运算，向量的加法与实数的加法类似，类比实数的减法运算，能否把向量的减法同样作为向量加法的逆运算引入呢？向量的减法具有什么特点？如何进行向量减法的运算呢？向量进行减法运算，必须先引入一个什么样的新概念？实例分析上周日杨恒从家骑车到八里河公园游玩,然后再由八里河公园返回家中,我们把八里河公园记作B点,杨恒家记作A点,那么杨恒的位移是多少?AB+BA=0AＢ怎样用向量来表示呢?我们把与a长度相等，方向相反的向量，叫作a的相反向量.记作1.相反向量－a，并且规定，零向量的相反向量仍是零向量．a和－a互为相反向量．请问的相反向量是AB:ABBA重要提示�______ba______,b______,ab,a)3(______a)a_____()a(a)2(______)a(11互为相反的向量，那么如果）（：练习a00ba0求两个向量差的运算,叫做向量的减法.2.向量的减法定义:向量加上的相反向量，叫作与的差，即()abab3.如何求两个向量的差？:向量减法的推导DEACBabbbaba()ababACADAEBC��ACABBC�即ACBabbaabOBAabab向量的减法：,,,,abOOAaOBbBAabababOAOBBA�����、内点，则与，记这减则已知向量在平面任取一作向量叫做的差作即种求向量差的方法，叫做向量法的三角形法。起点相同指向被减向量OabABba小结:作两向量的差向量的步骤:(1)将两向量移到共同起点(2)连接两向量的终点,方向指向被减向量注意与作和向量的区别即=__________ADAB1、DBCAAC00__________BCBA2、__________BABC3、__________CDBDACAB4、_________MPMNQPNQ5、练习2：例1已知向量a,b,c,求作向量a-b+c.abc。则作，作在平面上任取一点解baBAbOBaOAO,,ＯＢＡ。则为邻边作和并以再作cbaBCBABDBADC，BCBAcBC,CD练习:如图：平行四边形ABCD中,用表示向量ABCD,aAB,bADba,.,DBACbaACab�;由向量的减法可得，.DBABADab�解：由向量加法的平行四边形法则，得例2已知|a|=6,|b|=8,且|a+b|=|a-b|,求|a-b|.则为邻边作和以作设解ABCD，ADABbADaAB,,ADBabCbaDBbaAC,则||||||||DBACbabaABAD，ABCD，ABCD为矩形所以四边形为平行四边形又因为四边形10||||1086||||||2222babaDBDBDB练习:如图：平行四边形ABCD中,用表示向量ABCD变式二:在本例中,当a,b满足什么条件时,|a+b|=|a-b|?变式三:在本例中,a+b与a-b有可能相等吗?变式一:在本例中,当a,b满足什么条件时,a+b与a-b相互垂直?,aAB,bADba,.,DBACbaACab�;由向量的减法可得，.DBABADab�解：由向量加法的平行四边形法则，得（|a|=|b|）（a，b互相垂直）（不可能， 对角线方...