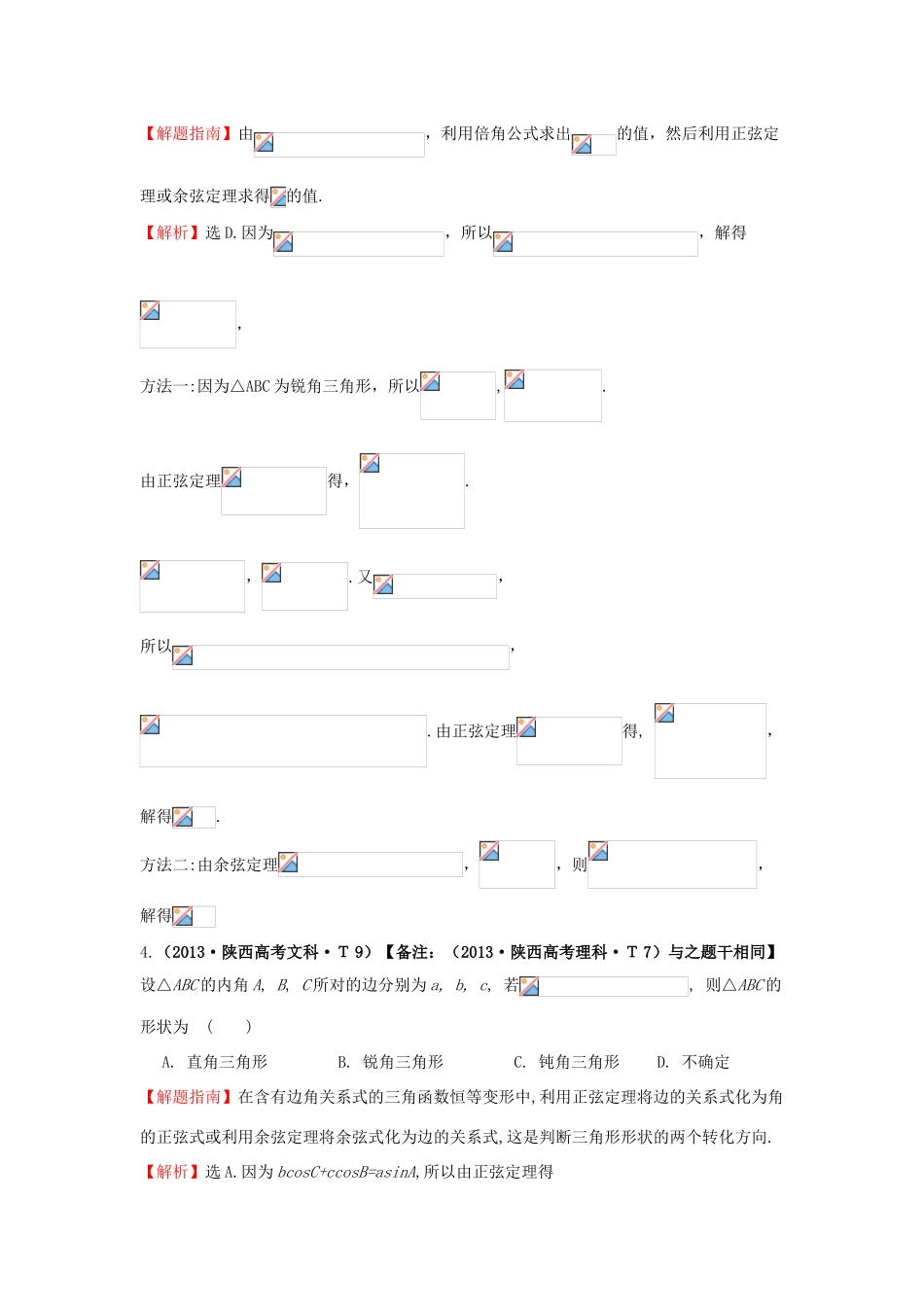
考点17正弦定理和余弦定理一、选择题1.(2013·北京高考文科·T5)在△ABC中,a=3,b=5,sinA=,则sinB=()A.B.C.D.1【解题指南】已知两边及一边的对角利用正弦定理求解。【解析】选B。由正弦定理得。2.(2013·新课标全国Ⅱ高考文科·T4)的内角的对边分别为,已知,,,则的面积为()A.B.C.D.【解题指南】利用正弦定理和三角形的面积公式可得【解析】选B.因为,所以.由正弦定理得,解得。所以三角形的面积为.因为,所以,选B.3.(2013·新课标Ⅰ高考文科·T10)已知锐角△ABC的内角A,B,C的对边分别为,,,,,c=6,则()A.10B.9C.8D.5【解题指南】由,利用倍角公式求出的值,然后利用正弦定理或余弦定理求得的值.【解析】选D.因为,所以,解得,方法一:因为△ABC为锐角三角形,所以,.由正弦定理得,.,.又,所以,.由正弦定理得,,解得.方法二:由余弦定理,,则,解得4.(2013·陕西高考文科·T9)【备注:(2013·陕西高考理科·T7)与之题干相同】设△ABC的内角A,B,C所对的边分别为a,b,c,若,则△ABC的形状为()A.直角三角形B.锐角三角形C.钝角三角形D.不确定【解题指南】在含有边角关系式的三角函数恒等变形中,利用正弦定理将边的关系式化为角的正弦式或利用余弦定理将余弦式化为边的关系式,这是判断三角形形状的两个转化方向.【解析】选A.因为bcosC+ccosB=asinA,所以由正弦定理得sinBcosC+sinCcosB=sin2A,所以sin(B+C)=sin2A,sinA=sin2A,sinA=1,所以三角形ABC是直角三角形.5.(2013·安徽高考文科·T9)【备注:(2013·安徽高考理科·T12)与之题干相同】设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,则3sinA=5sinB,则角C=()A.B.C.D.【解题指南】根据正弦定理、余弦定理进行解三角形计算。【解析】选B.由题设条件可得,由余弦定理得,所以。6.(2013·山东高考文科·T7)的内角的对边分别是,若,,,则()A.B.2C.D.1【解析】选B.由,则,由正弦定理知,即,所以cosA=,所以A=,,所以,所以,c=2.7.(2013·湖南高考理科·T3)在锐角中,角所对的边长分别为.若()A.B.C.D.【解题指南】本题先利用正弦定理化简条件等式,注意条件“锐角三角形”.【解析】选D.由2asinB=b得2sinAsinB=sinB,得sinA=,所以锐角A=.8.(2013·天津高考理科·T6)在△ABC中,则=()A.B.C.D.【解题指南】先由余弦定理求AC边长,然后根据正弦定理求值.【解析】选C.在△ABC中,由余弦定理得,所以由正弦定理得即所以.9.(2013·湖南高考文科·T5)在锐角ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于()A.B.C.D.【解题指南】本题先利用正弦定理化简条件等式,注意条件“锐角三角形”.【解析】选A.由2asinB=b得2sinAsinB=sinB,得sinA=,所以锐角A=.二、填空题10.(2013·浙江高考理科·T16)在△ABC中,∠C=90°,M是BC的中点.若,则sin∠BAC=.【解题指南】分别在Rt△ABC和△ABM中应用勾股定理和正弦定理.【解析】设AC=b,AB=c,BC=a,在△ABM中由正弦定理得①,因为,又,,所以.又由①得,两边平方化简得4c4-12a2c2+9a4=0,所以2c2-3a2=0,所以.【答案】11.(2013·上海高考理科·T4)已知△ABC的内角A,B,C所对应边分别为a,b,c,若3a2+2ab+3b2-3c2=0,则角C的大小是(结果用反三角函数值表示).【解析】3a2+2ab+3b2-3c2=0c⇒2=a2+b2+ab,故.【答案】12.(2013·上海高考文科·T5)已知ABC的内角A、B、C所对的边分别是a、b、c.若a2+ab+b2-c2=0,则角C的大小是.【解析】【答案】三、解答题13.(2013·大纲版全国卷高考文科·T18)与(2013·大纲版全国卷高考理科·T18)相同设的内角,,的对边分别为,(I)求;(II)若,求.【解题指南】(I)由条件确定求应采用余弦定理.(II)应用三角恒等变换求出及的值,列出方程组确定的值.【解析】(I)因为.所以.由余弦定理得,因此.(II)由(I)知,所以.故或,因此或14.(2013·新课标Ⅰ高考理科·T17)如图,在中,,,,为内一点,.(Ⅰ)若,求;(Ⅱ)若,求.【解析】由已知得,,所以.在,由余弦定理得,故.(Ⅱ)设,由已知得,在中,由正弦定理得,化简得,所以,即.15.(2013·天津高考文科·T16)在△ABC中,内角A,B,C所对的边分别是a,b,c....