辽宁省大连市真金教育信息咨询有限公司高三数学 第02章 函数的图像精炼试题 新人教A版 VIP免费

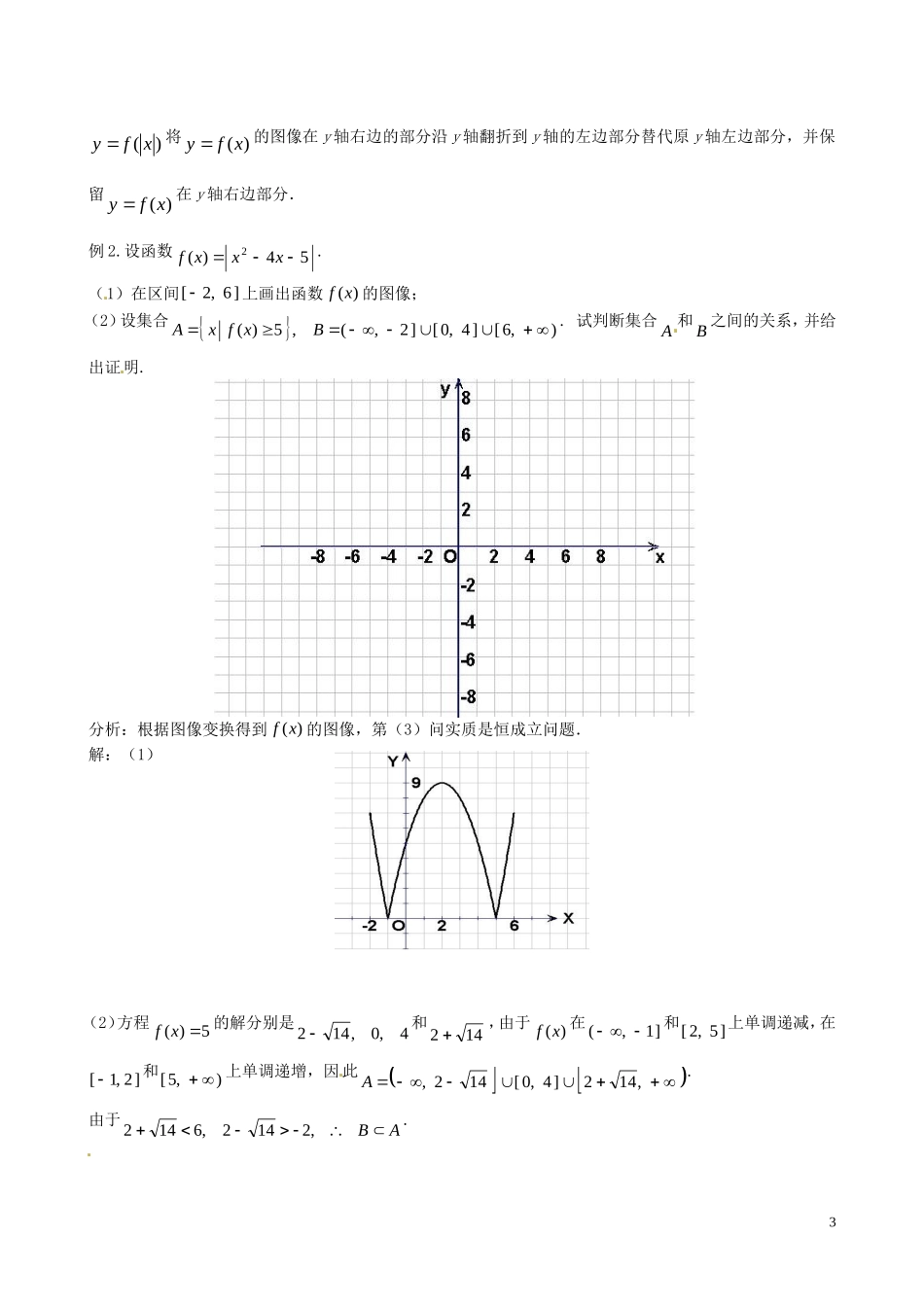
"辽宁省大连市真金教育信息咨询有限公司高三数学第02章函数的图像精炼【考点导读】1.掌握基本初等函数的图像特征，学会运用函数的图像理解和研究函数的性质；2.掌握画图像的基本方法：描点法和图像变换法．【基础练习】1.根据下列各函数式的变换，在箭头上填写对应函数图像的变换：（1）2xy12xy123xy；（2）2logyx2log()yx2log(3)yx．2.作出下列各个函数图像的示意图：（1）31xy；（2）2log(2)yx；（3）21xyx．解：（1）将3xy的图像向下平移1个单位，可得31xy的图像．图略；（2）将2logyx的图像向右平移2个单位，可得2log(2)yx的图像．图略；（3）由21111xyxx，将1yx的图像先向右平移1个单位，得11yx的图像，再向下平移1个单位，可得21xyx的图像．如下图所示：3.作出下列各个函数图像的示意图：（1）12log()yx；（2）1()2xy；（3）12logyx；（4）21yx．解：（1）作12logyx的图像关于y轴的对称图像，如图1所示；（2）作1()2xy的图像关于x轴的对称图像，如图2所示；（3）作12logyx的图像及它关于y轴的对称图像，如图3所示；（4）作21yx的图像，并将x轴下方的部分翻折到x轴上方，如图4所示．1Oyx1－1－1Oyx图1－1Oyx图2－1Oyx图31向右平移1个单位向上平移3个单位作关于y轴对称的图形向右平移3个单位－1Oyx图44.函数()|1|fxx的图象是（B）【范例解析】例1.作出函数2()223fxxx及()fx，()fx，(2)fx，()fx，()fx的图像．分析：根据图像变换得到相应函数的图像．解：()yfx与()yfx的图像关于y轴对称；()yfx与()yfx的图像关于x轴对称；将()yfx的图像向左平移2个单位得到(2)yfx的图像；保留()yfx的图像在x轴上方的部分，将x轴下方的部分关于x轴翻折上去，并去掉原下方的部分；将()yfx的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分，并保留()yfx在y轴右边部分．图略．点评：图像变换的类型主要有平移变换，对称变换两种．平移变换：左“+”右“－”，上“+”下“－”；对称变换：()yfx与()yfx的图像关于y轴对称；()yfx与()yfx的图像关于x轴对称；()yfx与()yfx的图像关于原点对称；()yfx保留()yfx的图像在x轴上方的部分，将x轴下方的部分关于x轴翻折上去，并去掉原下方的部分；2A1xyOB1xyOC1xyOD1xyO-1-1-1-11111()yfx将()yfx的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分，并保留()yfx在y轴右边部分．例2.设函数54)(2xxxf.（1）在区间]6,2[上画出函数)(xf的图像；（2）设集合),6[]4,0[]2,(,5)(BxfxA.试判断集合A和B之间的关系，并给出证明.分析：根据图像变换得到)(xf的图像，第（3）问实质是恒成立问题．解：（1）（2）方程5)(xf的解分别是4,0,142和142，由于)(xf在]1,(和]5,2[上单调递减，在]2,1[和),5[上单调递增，因此,142]4,0[142,A.由于AB,2142,6142.3【反馈演练】2.为了得到函数xy)31(3的图象，可以把函数xy)31(的图象向右平移1个单位长度得到．3．已知函数kxyxy与41log的图象有公共点A，且点A的横坐标为2，则k=14．4．设f(x)是定义在R上的奇函数，且y=f(x)的图象关于直线21x对称，则f(1)+f(2)+f(3)+f(4)+f(5)=_____0____．5.作出下列函数的简图：（1）2(1)yxx；（2）21xy；（3）2log21yx．45