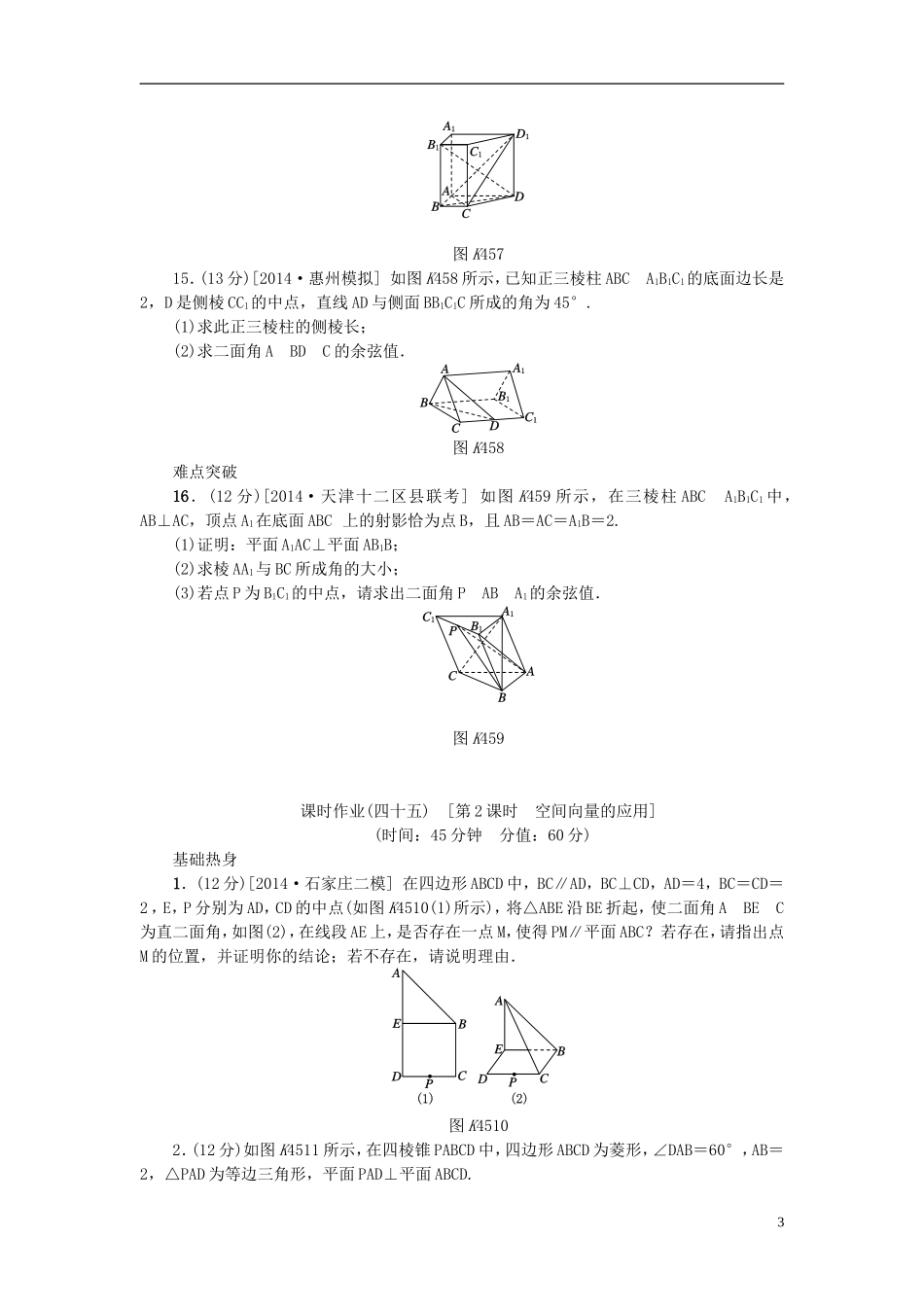
课时作业(四十五)[第45讲第1课时空间角的求法](时间:45分钟分值:100分)基础热身1.若向量a=(1,λ,2),b=(2,-1,2),且cos〈a,b〉=,则λ=()A.2B.-2C.-2或D.2或-2.如图K451所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则BC1与AB1所成角的余弦值为()图K451A.B.C.D.3.在空间直角坐标系Oxyz中,平面OAB的法向量为n=(2,-2,1),已知P(-1,3,2),则点P到平面OAB的距离d等于()A.4B.2C.3D.14.如图K452所示,在正方体ABCDA1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为()A.30°B.45°C.60°D.90°图K452图K4535.如图K453所示,直三棱柱ABCA1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为________.图K4546.如图K454所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos〈DP,AE〉=.若以DA,DC,DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则点E的坐标为___1_____________________________________________________________________.能力提升7.[2014·沈阳调研]在直三棱柱A1B1C1ABC中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是()A.B.C.D.8.如图K455所示,正四棱锥SABCD的侧棱长为,底面边长为,E为SA的中点,则异面直线BE与SC所成的角是()A.30°B.45°C.60°D.90°图K455图K4569.如图K456所示,已知正三棱柱ABCA1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的正弦值为()A.B.C.D.10.[2014·皖北五校联考]在正三棱柱ABCA1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为()A.B.-C.D.-11.已知三棱锥OABC的侧棱OA,OB,OC两两垂直,E为OC的中点,且OA=1,OB=OC=2,则平面EAB与平面ABC所成角的余弦值是()A.B.C.D.12.[2014·佛山质检]已知棱长为1的正方体ABCDA1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.13.[2014·合肥调研]已知在长方体ABCDA1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是________.14.(10分)如图K457所示,在直棱柱ABCDA1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.(1)证明:AC⊥B1D;(2)求直线B1C1与平面ACD1所成角的正弦值.2图K45715.(13分)[2014·惠州模拟]如图K458所示,已知正三棱柱ABCA1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.(1)求此正三棱柱的侧棱长;(2)求二面角ABDC的余弦值.图K458难点突破16.(12分)[2014·天津十二区县联考]如图K459所示,在三棱柱ABCA1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.(1)证明:平面A1AC⊥平面AB1B;(2)求棱AA1与BC所成角的大小;(3)若点P为B1C1的中点,请求出二面角PABA1的余弦值.图K459课时作业(四十五)[第2课时空间向量的应用](时间:45分钟分值:60分)基础热身1.(12分)[2014·石家庄二模]在四边形ABCD中,BC∥AD,BC⊥CD,AD=4,BC=CD=2,E,P分别为AD,CD的中点(如图K4510(1)所示),将△ABE沿BE折起,使二面角ABEC为直二面角,如图(2),在线段AE上,是否存在一点M,使得PM∥平面ABC?若存在,请指出点M的位置,并证明你的结论;若不存在,请说明理由.图K45102.(12分)如图K4511所示,在四棱锥PABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.3(1)求证:AD⊥PB.(2)在棱AB上是否存在点F,使DF与平面PDC所成角的正弦值为?若存在,确定线段AF的长度;若不存在,请说明理由.图K4511能力提升3.(12分)[2014·北京东城区模拟]如图K4512所示,四棱锥EABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.(1)求证:BD⊥平面ADE.(2)求BE和平面CDE所成角的正弦值.(3)在线段CE上是否存在一点F,使得平面BDF⊥平面CDE?请说明理由.图K45124.(12分)如图K4513所示,三棱柱ABCA1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1...