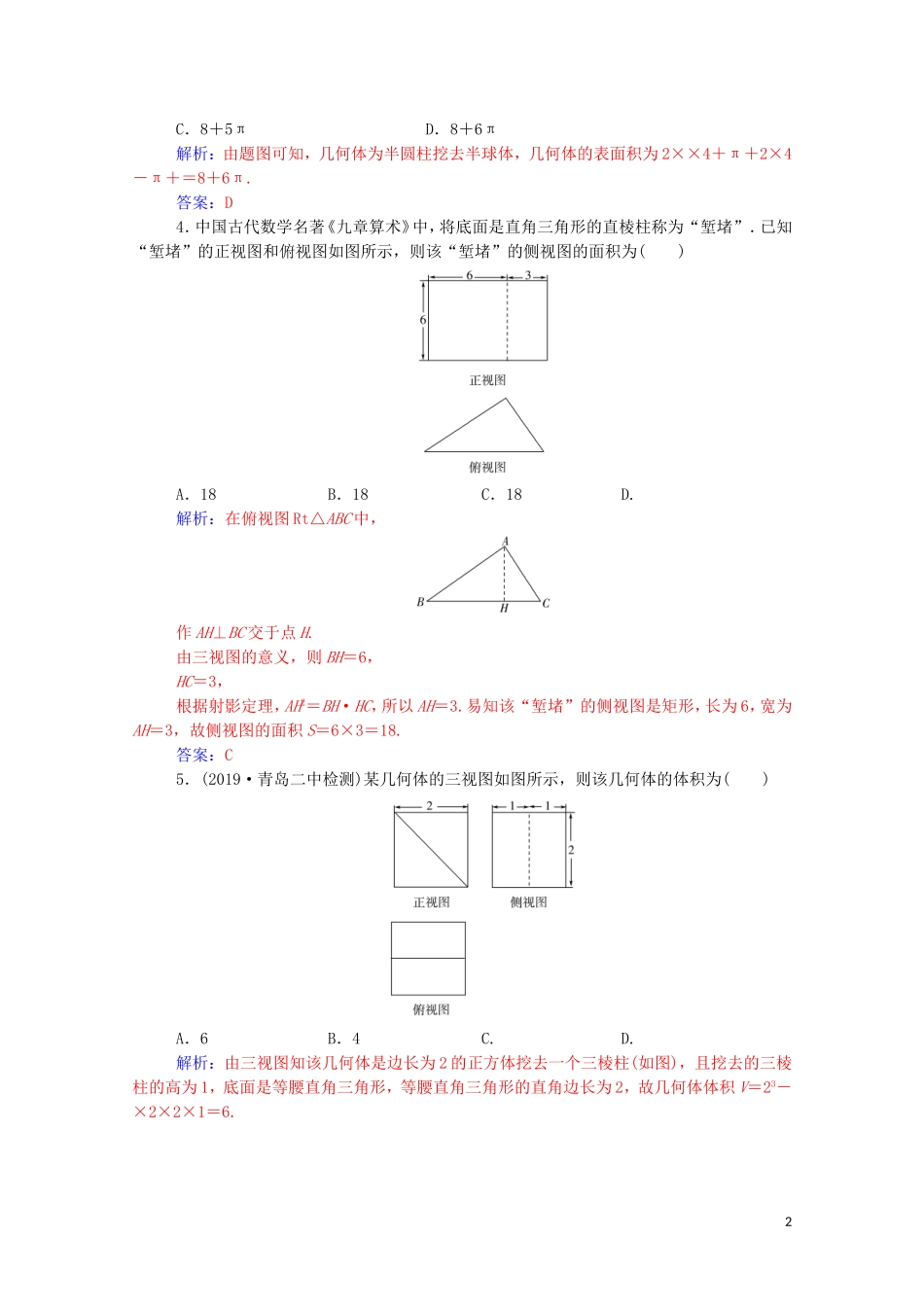
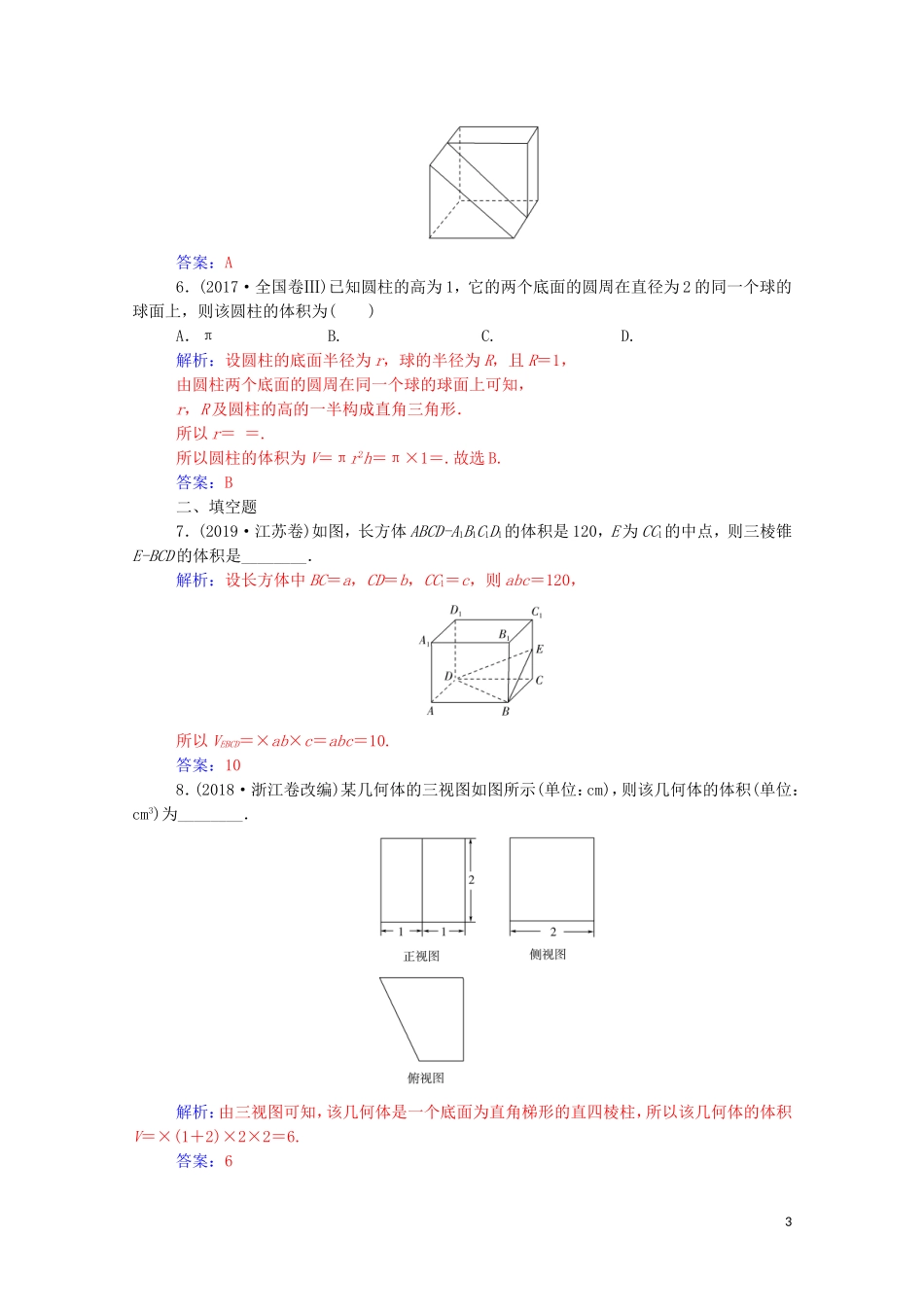
第1讲空间几何体的三视图、表面积及体积A级基础通关一、选择题1.半径为R的半圆卷成一个圆锥,则它的体积为()A.πR3B.πR3C.πR3D.πR3解析:设圆锥的底面圆的半径为r,高为h,由2πr=πR,得r=,因此h==R.所以V圆锥=πr2·h=π··R=πR3.答案:B2.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.4解析:由三视图得到空间几何体,如图所示,则PA⊥平面ABCD,平面ABCD为直角梯形,PA=AB=AD=2,BC=1,所以PA⊥AD,PA⊥AB,PA⊥BC.又BC⊥AB,AB∩PA=A,所以BC⊥平面PAB,所以BC⊥PB.在△PCD中,PD=2,PC=3,CD=,所以△PCD为锐角三角形.所以侧面中的直角三角形为△PAB,△PAD,△PBC,共3个.答案:C3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.8+3πB.8+4π1C.8+5πD.8+6π解析:由题图可知,几何体为半圆柱挖去半球体,几何体的表面积为2××4+π+2×4-π+=8+6π.答案:D4.中国古代数学名著《九章算术》中,将底面是直角三角形的直棱柱称为“堑堵”.已知“堑堵”的正视图和俯视图如图所示,则该“堑堵”的侧视图的面积为()A.18B.18C.18D.解析:在俯视图Rt△ABC中,作AH⊥BC交于点H.由三视图的意义,则BH=6,HC=3,根据射影定理,AH2=BH·HC,所以AH=3.易知该“堑堵”的侧视图是矩形,长为6,宽为AH=3,故侧视图的面积S=6×3=18.答案:C5.(2019·青岛二中检测)某几何体的三视图如图所示,则该几何体的体积为()A.6B.4C.D.解析:由三视图知该几何体是边长为2的正方体挖去一个三棱柱(如图),且挖去的三棱柱的高为1,底面是等腰直角三角形,等腰直角三角形的直角边长为2,故几何体体积V=23-×2×2×1=6.2答案:A6.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.C.D.解析:设圆柱的底面半径为r,球的半径为R,且R=1,由圆柱两个底面的圆周在同一个球的球面上可知,r,R及圆柱的高的一半构成直角三角形.所以r==.所以圆柱的体积为V=πr2h=π×1=.故选B.答案:B二、填空题7.(2019·江苏卷)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是________.解析:设长方体中BC=a,CD=b,CC1=c,则abc=120,所以VEBCD=×ab×c=abc=10.答案:108.(2018·浙江卷改编)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)为________.解析:由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V=×(1+2)×2×2=6.答案:639.(2017·北京卷改编)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为________.解析:根据三视图可得该四棱锥的直观图(四棱锥P-ABCD)如图所示,将该四棱锥放入棱长为2的正方体中.由图可知该四棱锥的最长棱为PD,PD==2.答案:210.(2019·惠州调研)已知一张矩形白纸ABCD,AB=10,AD=10,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,使A,C重合于点P,则三棱锥PDEF的外接球的表面积为________.解析:三棱锥P-DEF中,PD2+PF2=CD2+CF2=DF2,所以∠DPF=90°,且DF2=102+(5)2=150.又∠DEF=90°,所以DF的中点为三棱锥PDEF的外接球的球心,则2R=DF,故球的表面积S=4πR2=150π.答案:150πB级能力提升11.(2019·雅礼中学质检)一个几何体的三视图如图所示,则该几何体的体积为()4A.B.5C.D.π解析:由三视图可知,该几何体是一个组合体,它由半个圆锥与四分之一球体组成,其中圆锥的底面半径为1,高为2,体积为××π×12×2=;球的半径为1,体积为×π×13=.所以该几何体的体积V=+=.答案:C12.我国齐梁时代的数学家祖暅提出了一条原理:“幂势既同,则积不容异”.意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图,将底面直径都为2b,高皆为a的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面β上,用平行于平面β且与平面β任意距离d...