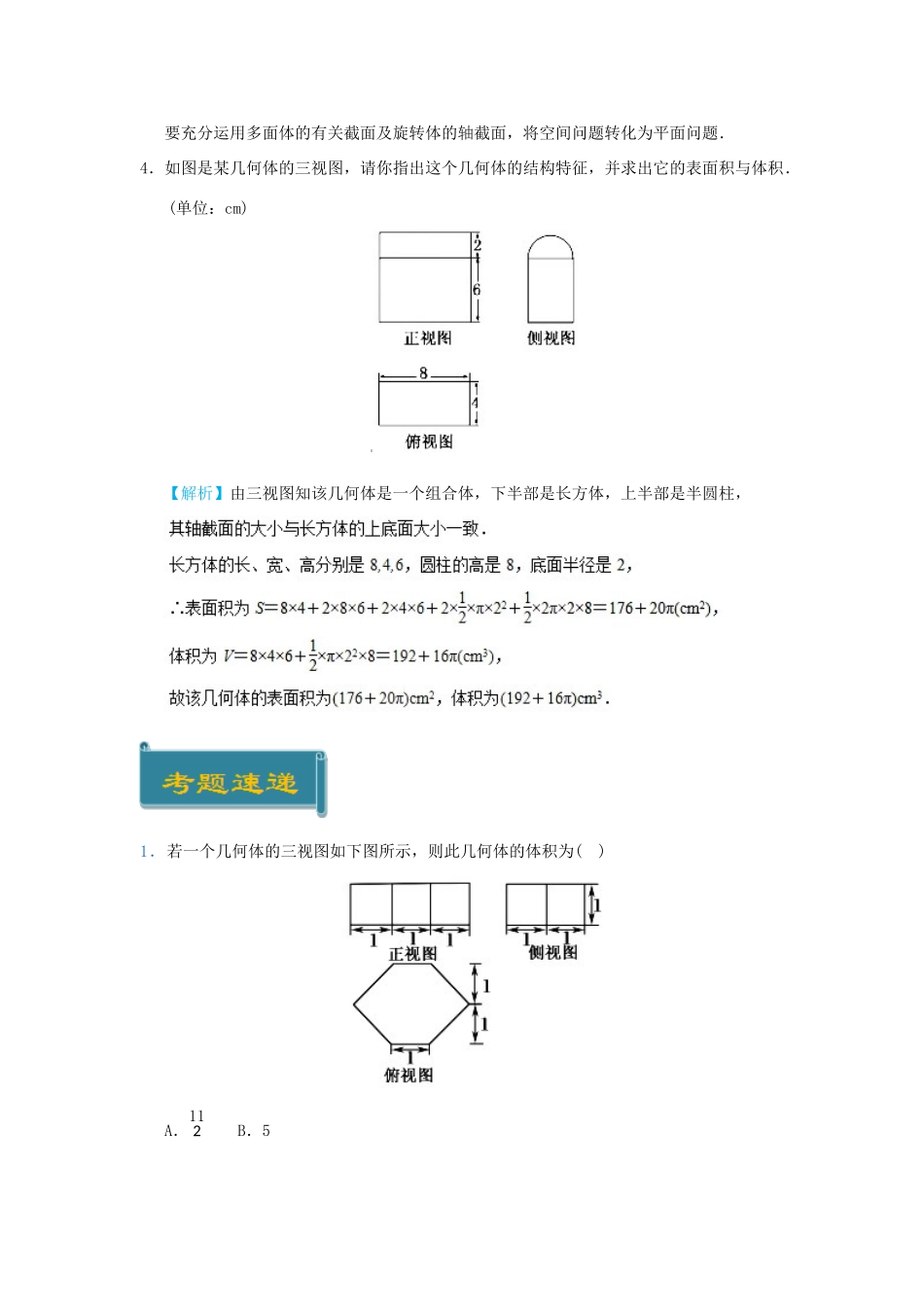
考点12柱体、锥体、台体的体积1.棱柱的体积公式为V柱体=Sh,(S为柱体底面积,h为柱体的高),.2.若一个棱锥的底面积为S,高为h,则它的体积是V锥体=13Sh,3.若一个台体上、下底面的面积分别为S′、S,高为h,则它的体积公式为V台体=13h(S++S′),4.圆柱的体积公式为V圆柱=πr2h(r为底面半径,h为圆柱的高).5.圆锥的底面半径为r,高为h,则它的体积为V圆锥=13πr2h.6.若圆台上、下底面半径分别为r′、r,高为h,则它的体积为V圆台=13πh(r2+rr′+r′2).【例】现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.【答案】1.圆台的体积为7π,上、下底面的半径分别为1和2,则圆台的高为()A.3B.4C.5D.6【答案】A【解析】由题意,V=13(π+2π+4π)h=7π,∴h=3.2.圆柱的侧面展开图是长12cm,宽8cm的矩形,则这个圆柱的体积为()A.288πcm3B.192πcm3C.288πcm3或192πcm3D.192πcm3【答案】C【解析】圆柱的高为8cm时,V=π×122π2×8=288πcm3.当圆柱的高为12cm时,V=π×82π2×12=192πcm3.【解题技巧】圆柱的侧面展开图是一个矩形,矩形两边长分别为圆柱底面周长和高;圆锥侧面展开图是一个扇形,半径为圆锥的母线,弧长为圆锥底面周长;圆台侧面展开图是一个扇环,其两段弧长为圆台两底周长,扇形两半径的差为圆台的母线长,对于柱、锥、台的有关问题,有时要通过侧面展开图来求解.3.已知一个母线长为1的圆锥的侧面展开图的圆心角等于240°,则该圆锥的体积为()A.281πB.881πC.581πD.1081π【答案】C【思路方法】计算柱体、锥体和台体的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面及旋转体的轴截面,将空间问题转化为平面问题.4.如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.(单位:cm)【解析】由三视图知该几何体是一个组合体,下半部是长方体,上半部是半圆柱,1.若一个几何体的三视图如下图所示,则此几何体的体积为()A.112B.5C.92D.4【答案】D【解析】易知该几何体是一个六棱柱,由三视图可得底面面积S底=1×2+4×12×1×1=4,高为1,故此几何体的体积V=4×1=4.2.某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.1【答案】A【解析】由三视图知,三棱锥如图所示:由侧视图得高h=1,又底面积S=12×1×1=12.所以体积V=13Sh=16.3.已知四棱锥P-ABCD的直观图及三视图如图所示,求该四棱锥的体积.【答案】23.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛【答案】B