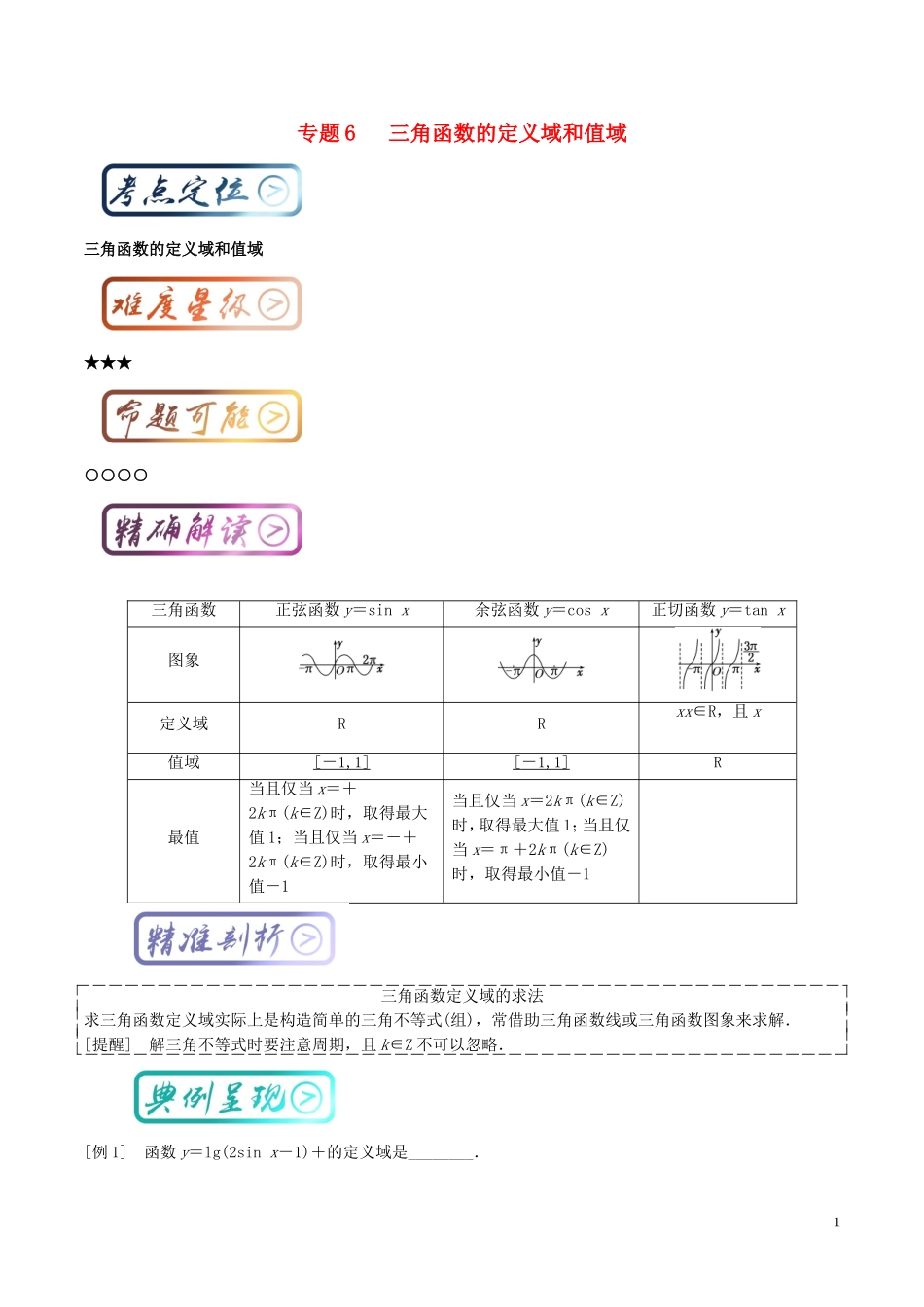
专题6三角函数的定义域和值域三角函数的定义域和值域★★★○○○○三角函数正弦函数y=sinx余弦函数y=cosx正切函数y=tanx图象定义域RRxx∈R,且x值域[-1,1][-1,1]R最值当且仅当x=+2kπ(k∈Z)时,取得最大值1;当且仅当x=-+2kπ(k∈Z)时,取得最小值-1当且仅当x=2kπ(k∈Z)时,取得最大值1;当且仅当x=π+2kπ(k∈Z)时,取得最小值-1三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.[提醒]解三角不等式时要注意周期,且k∈Z不可以忽略.[例1]函数y=lg(2sinx-1)+的定义域是________.11.函数y=2sin(0≤x≤9)的最大值与最小值之和为()A.2-B.0C.-1D.-1-[解析]∵0≤x≤9,∴-≤x-≤,∴sin∈.∴y∈[-,2],∴ymax+ymin=2-.(2)函数y=3-sinx-2cos2x,x∈的值域为________.[解析]∵x∈,∴sinx∈.又y=3-sinx-2cos2x=3-sinx-2(1-sin2x)=22+,∴当sinx=时,ymin=;当sinx=-或sinx=1时,ymax=2.故该函数的值域为.1.函数y=的定义域为()A.B.(k∈Z)C.(k∈Z)D.R解析:选C要使函数有意义,则cosx-≥0,即cosx≥,解得2kπ-≤x≤2kπ+,k∈Z.2.函数f(x)=sin在区间上的最小值为()A.-1B.-C.0D.解析:选B因为0≤x≤,所以-≤2x-≤,由正弦函数的图象知,-≤sin≤1,所以函数f(x)=sin在区间上的最小值为-.23.函数y=的定义域为________.4.函数y=lg(sin2x)+的定义域为________.解析:由得∴-3≤x<-或0