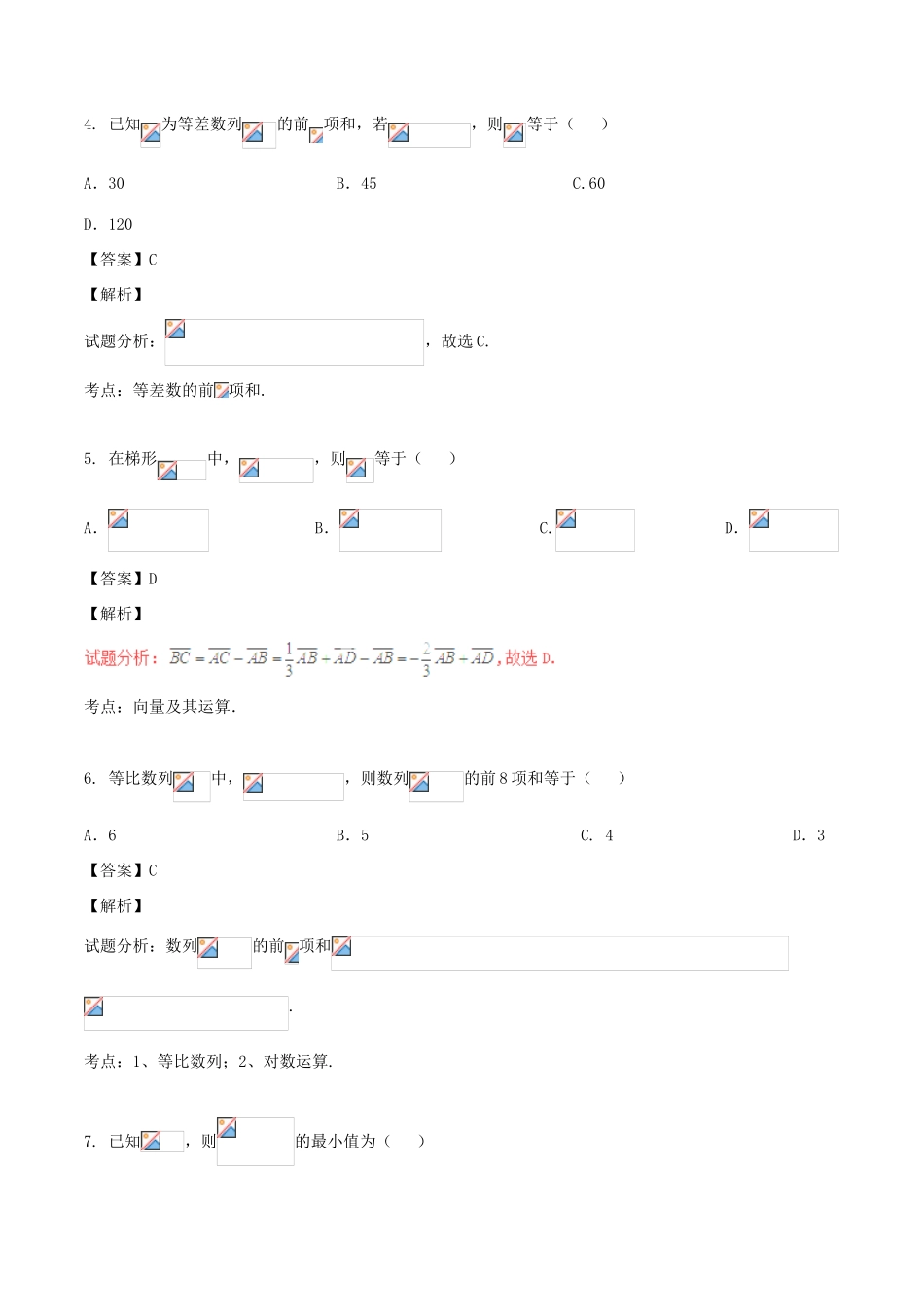
专题24综合训练31.已知集合,,则等于()A.B.C.D.【答案】C【解析】试题分析:集合、的公共元素是,所以选C.考点:集合的基本运算.2.的值为()A.B.C.D.【答案】A【解析】考点:诱导公式.3.下列各图中,表示以为自变量的奇函数的图象是()A.B.C.D.【答案】B【解析】试题分析:作平行于轴的直线,图象中的取值是唯一的,故排除A,D,奇函数的图象关于原点对称,故选B.考点:1、函数的奇偶性;2、函数的定义.4.已知为等差数列的前项和,若,则等于()A.30B.45C.60D.120【答案】C【解析】试题分析:,故选C.考点:等差数的前项和.5.在梯形中,,则等于()A.B.C.D.【答案】D【解析】考点:向量及其运算.6.等比数列中,,则数列的前8项和等于()A.6B.5C.4D.3【答案】C【解析】试题分析:数列的前项和.考点:1、等比数列;2、对数运算.7.已知,则的最小值为()A.B.4C.D.【答案】D【解析】试题分析:,,故选D.考点:基本不等式.【方法点晴】本题主要考查的基本不等式,属于容易题.但是本题比较容易犯错,使用该公式时一定要牢牢抓住一正、二定、三相等这三个条件,如果不符合条件则:非正化正、非定构定、不等作图(单调性).平时应熟练掌握双钩函数的图象,还应加强非定构定、不等作图这方面的训练,并注重表达的规范性,才能灵活应对这类题型.8.已知为单位向量,且,向量满足,则的范围为()A.B.C.D.【答案】B【解析】考点:向量及其运算性质.9.已知两定点和,动点在直线上移动,椭圆以为焦点且经过点,则椭圆的离心率的最大值为()A.B.C.D.【答案】A【解析】试题分析:关于直线的对称点为,连接交直线于点,则椭圆的长轴长的最小值为,所以椭圆的离心率的最大值为,故选A.考点:1、椭圆的离心率;2、点关于直线的对称.10.已知偶函数对于任意的满足,(其中是函数的导函数),则下列不等式中成立的是()A.B.C.D.【答案】D【解析】考点:1、函数的导数;2、函数的单调性.【方法点晴】本题考查函数的导数、函数的单调性,涉及函数与不等式思想、数形结合思想和转化化归思想,考查逻辑思维能力、等价转化能力、运算求解能力,综合性较强,属于较难题型.首先构造函数在为增函数,构造函数是本题的突破口.11.定义,已知实数满足,设,则的取值范围是()A.B.C.D.【答案】A【解析】xyo考点:线性规划.【方法点晴】本题考查线性规划问题,灵活性较强,属于较难题型.考生应注总结解决线性规划问题的一般步骤:(1)在直角坐标系中画出对应的平面区域,即可行域;(2)由目标函数变形为;(3)作平行线:将直线平移,使直线与可行域有交点,且观察在可行域中使最大(或最小)时所经过的点,求出该点的坐标;(4)求出最优解:将(3)中求出的坐标代入目标函数,从而求出的最大(小)值.12.将圆的一组等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录个点的颜色,称为该圆的一个“阶段序”,当且仅当两个阶色序对应位置上的颜色至少有一个不相同时,称为不同的阶色序.若某圆的任意两个“阶段序”均不相同,则称该圆为“阶魅力圆”.“3阶魅力xyo圆”中最多可有的等分点个数为()A.4B.6C.8D.10【答案】C【解析】考点:排列组合.