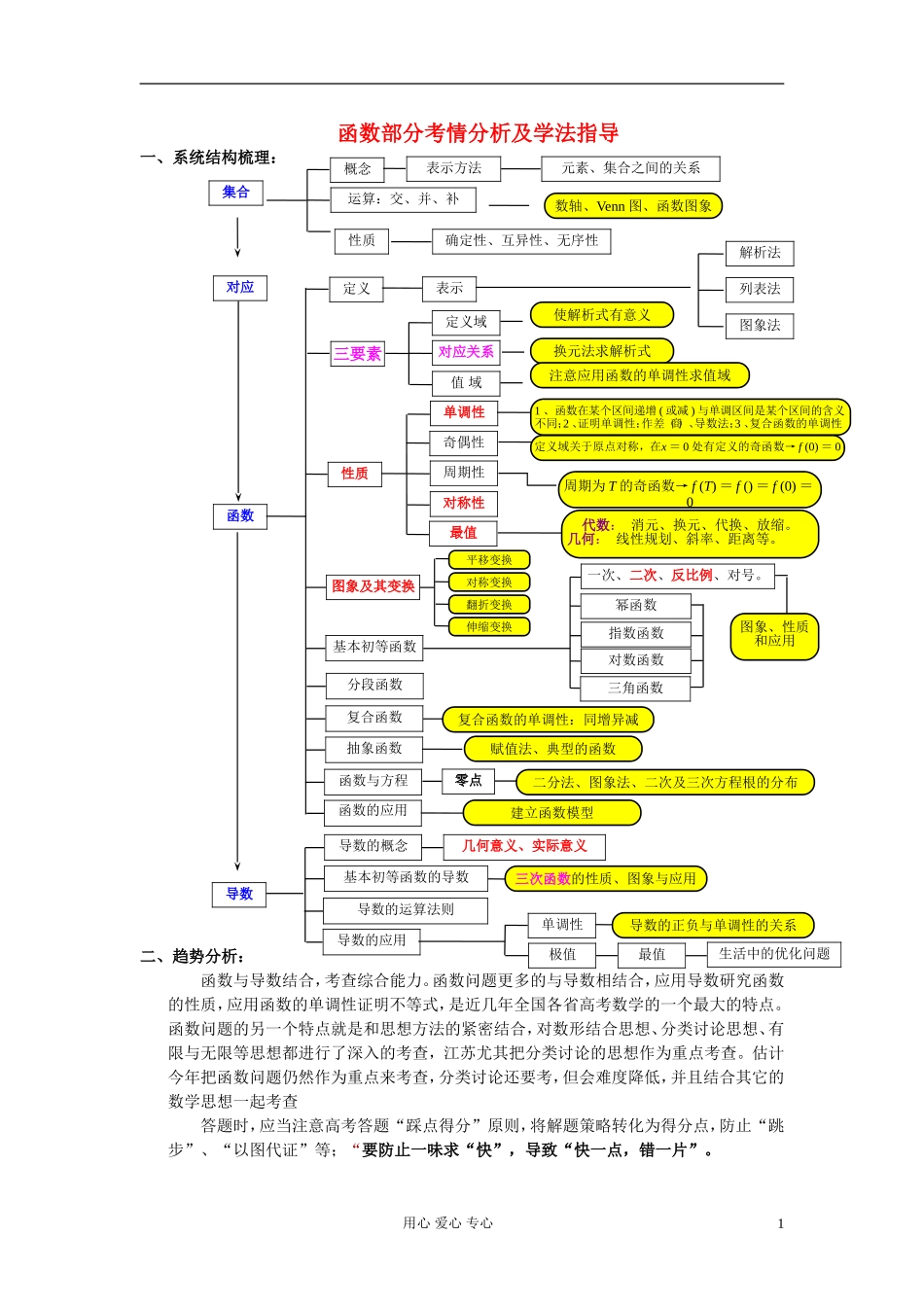
函数部分考情分析及学法指导一、系统结构梳理:二、趋势分析:函数与导数结合,考查综合能力。函数问题更多的与导数相结合,应用导数研究函数的性质,应用函数的单调性证明不等式,是近几年全国各省高考数学的一个最大的特点。函数问题的另一个特点就是和思想方法的紧密结合,对数形结合思想、分类讨论思想、有限与无限等思想都进行了深入的考查,江苏尤其把分类讨论的思想作为重点考查。估计今年把函数问题仍然作为重点来考查,分类讨论还要考,但会难度降低,并且结合其它的数学思想一起考查答题时,应当注意高考答题“踩点得分”原则,将解题策略转化为得分点,防止“跳步”、“以图代证”等;“要防止一味求“快”,导致“快一点,错一片”。用心爱心专心1集合对应概念元素、集合之间的关系运算:交、并、补数轴、Venn图、函数图象性质确定性、互异性、无序性定义表示解析法列表法三要素图象法定义域对应关系值域性质奇偶性周期性对称性单调性定义域关于原点对称,在x=0处有定义的奇函数→f(0)=01、函数在某个区间递增(或减)与单调区间是某个区间的含义不同;2、证明单调性:作差(商)、导数法;3、复合函数的单调性最值代数:消元、换元、代换、放缩。几何:线性规划、斜率、距离等。幂函数对数函数三角函数基本初等函数抽象函数复合函数赋值法、典型的函数函数与方程二分法、图象法、二次及三次方程根的分布零点函数的应用建立函数模型使解析式有意义导数函数基本初等函数的导数导数的概念导数的运算法则导数的应用表示方法换元法求解析式分段函数几何意义、实际意义单调性导数的正负与单调性的关系生活中的优化问题注意应用函数的单调性求值域周期为T的奇函数→f(T)=f()=f(0)=0复合函数的单调性:同增异减三次函数的性质、图象与应用一次、二次、反比例、对号。指数函数图象、性质和应用平移变换对称变换翻折变换伸缩变换图象及其变换最值极值