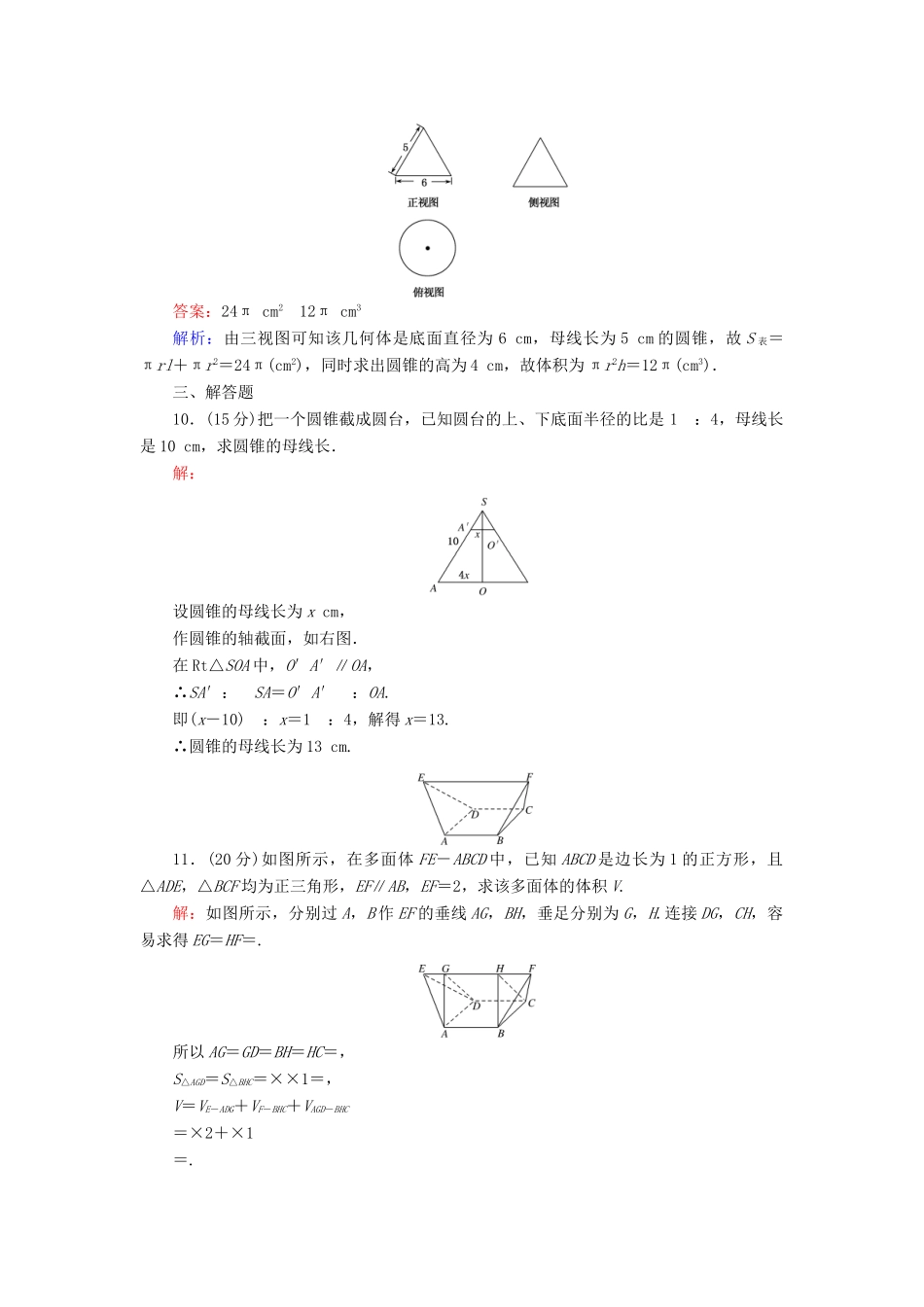
习题课空间几何体一、选择题(每个5分,共30分)1.一个几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.1答案:C解析:由三视图可知该几何体是由一个正方体截去一个三棱锥而得到,其直观图如图所示,其中正方体的棱长为1,则正方体的体积为1,截掉的三棱锥的体积为××1×1×1=,所以该几何体的体积为1-=,选C.2.下列四个命题中正确命题的个数是()①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体A.3B.2C.1D.0答案:C解析:本题主要涉及到直平行六面体、长方体的概念问题.如果底面是矩形但侧棱不垂直于底面,这时的四棱柱就不是直平行六面体,所以命题①是错误命题.如果底面是菱形,底面边长与棱长相等的直四棱柱不是正方体,所以命题②是错误命题.命题③也是错误命题,因为若两条侧棱垂直于底面一边可推出两个相对侧面是矩形,但是不能推出侧棱与底面垂直.命题④是正确命题,由对角线相等,可得出平行六面体的对角面是矩形,从而推得侧棱与底面垂直,这个平行六面体是直平行六面体.故选C.3.已知某圆柱的侧面展开图是边长为2a,a的矩形,则该圆柱的体积为()A.或B.C.D.或答案:A解析:设圆柱的母线长为l,底面圆的半径为r,则当l=2a时,2πr=a,∴r=,这时V圆柱=2a·π2=;当l=a时,2πr=2a,∴r=,这时V圆柱=a·π2=.综上,该圆柱的体积为或.4.一个圆锥的底面积为9π,母线长为5,则它的高为()A.4B.3C.D.答案:A解析:易知底面圆的半径r=3,由勾股定理h2+r2=l2,得h=4.5.有下列命题:①从投影的角度看,三视图画出的直观图是在平行投影下画出来的空间图形;②平行投影的投影线互相平行,中心投影的投影线相交于一点;③空间几何体在平行投影与中心投影下有不同的表现形式.其中正确的命题有()A.1个B.2个C.3个D.0个答案:D6.甲、乙、丙、丁四人分别面对面地坐在一张四方形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“6”丙说他看到的是“9”,丁说他看到的是“9”则下列说法中正确的是()A.甲在丁的对面,乙在甲的左边,丙在丁的右面B.丙在乙的对面,丙的左边是甲,右边是乙C.甲在乙的对面,甲的右边是丙,左边是丁D.甲在丁的对面,乙在甲的右边,丙在丁的右边答案:D解析:桌上一张纸上写着数字9,则看到9的人应坐在桌子的正面,看到6的人应坐在他的对面,如图所示.由此便可判断乙在左侧,而丙应在右侧.所以乙应在甲的右边.所以选D.二、填空题(每个5分,共15分)7.用6根长度相等的火柴搭成边长等于火柴长的正三角形,最多能搭成________个.答案:4解析:考虑正四面体8.已知半径为5的球的两个平行截面圆的周长分别为6π和8π,则这两个截面间的距离为________.答案:1或7解析:若两个平行截面在球心的同侧,则两个截面间的距离为-=1;若两个平行截面在球心的异侧,则两个截面间的距离为+=7.9.一个几何体的三视图及其尺寸(单位:cm)如图所示,则该几何体的表面积是________,体积是________.答案:24πcm212πcm3解析:由三视图可知该几何体是底面直径为6cm,母线长为5cm的圆锥,故S表=πrl+πr2=24π(cm2),同时求出圆锥的高为4cm,故体积为πr2h=12π(cm3).三、解答题10.(15分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长是10cm,求圆锥的母线长.解:设圆锥的母线长为xcm,作圆锥的轴截面,如右图.在Rt△SOA中,O′A′∥OA,∴SA′:SA=O′A′:OA.即(x-10):x=1:4,解得x=13.∴圆锥的母线长为13cm.11.(20分)如图所示,在多面体FE-ABCD中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,求该多面体的体积V.解:如图所示,分别过A,B作EF的垂线AG,BH,垂足分别为G,H.连接DG,CH,容易求得EG=HF=.所以AG=GD=BH=HC=,S△AGD=S△BHC=××1=,V=VE-ADG+VF-BHC+VAGD-BHC=×2+×1=.12.(20分)如图,在正三棱锥P-ABC中,∠APB=30°,侧棱长为a,E,F分别是PB,PC上的点,...