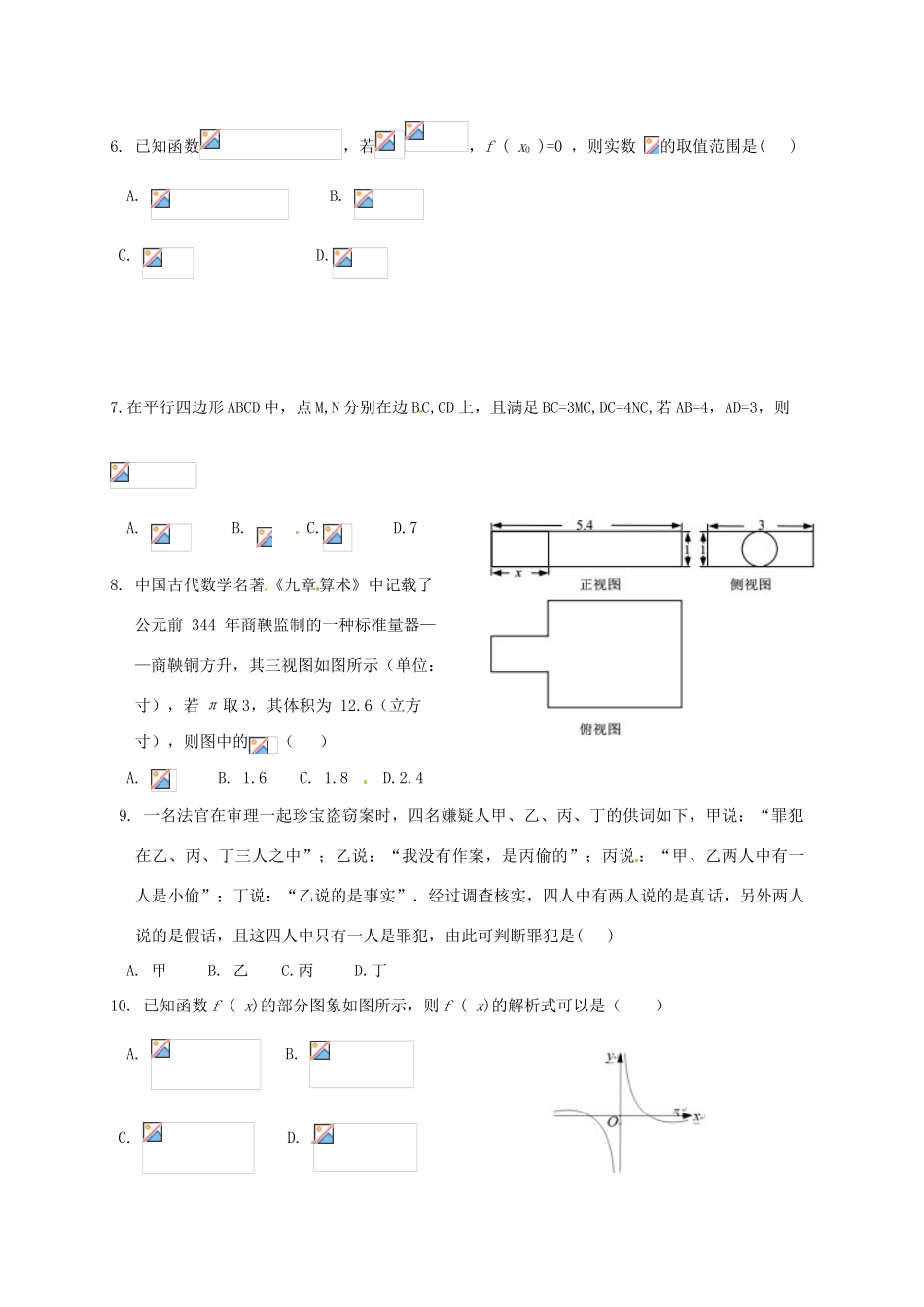
武昌区2017届高三年级元月调研考试文科数学第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合,则()A.B.C.D.2.在复平面内,复数(i为虚数单位)的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.若满足约束条件,则的最大值为()A.-3B.C.1D.4.执行如图所示的程序框图,若输入的,则输出的()A.2B.3C.4D.55.设公比为且的等比数列的前项和为,若,则()A.-2B.-1C.D.6.已知函数,若,f(x0)=0,则实数的取值范围是()A.B.C.D.7.在平行四边形ABCD中,点M,N分别在边BC,CD上,且满足BC=3MC,DC=4NC,若AB=4,AD=3,则A.B.C.D.78.中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的()A.B.1.6C.1.8D.2.49.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、丁的供词如下,甲说:“罪犯在乙、丙、丁三人之中”;乙说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一人是小偷”;丁说:“乙说的是事实”.经过调查核实,四人中有两人说的是真话,另外两人说的是假话,且这四人中只有一人是罪犯,由此可判断罪犯是()A.甲B.乙C.丙D.丁10.已知函数f(x)的部分图象如图所示,则f(x)的解析式可以是()A.B.C.D.11.已知是椭圆与双曲线的公共焦点,P是它们的一个公共点,且,线段的垂直平分线过,若椭圆的离心率为,双曲线的离心率为,则的最小值为()A.6B.3C.D.12.若在区间上是增函数,则实数的取值范围是()A.B.C.D.第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知直线将圆平分,且与直线垂直,则的方程为.14.某射击运动员每次射击击中目标的概率为80%,现采用随机模拟的方法估计该运动员4次射击至少3次击中目标的概率:先由计算器产生0—9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;再以每4个随机数为一组,代表4次射击记过,敬随机模拟产生了如下20组随机数:据此估计,该射击运动员4次射击至少3次击中目标的概率为.15.等差数列的前项和为已知为整数,且则数列的前项和为.16.在矩形ABCD中,现将沿沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,给出下列结论:①存在某个位置,使得直线AC与直线BD垂直;②存在某个位置,使得直线AB与直线CD垂直;③存在某个位置,使得直线AD与直线BC垂直.其中正确的结论序号为.(写出所有正确结论的序号)三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.(本题满分10分)的内角的对边分别为,已知(1)求B;(2)若,求的面积.18.(本题满分12分)如图,四棱锥中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.(Ⅰ)证明:SD⊥平面SAB;(Ⅱ)求四棱锥的高.19.(本题满分12分)我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(Ⅲ)若该市政府希望85%的居民每月的用水量不超过标准(吨),估计的值,并说明理由.20.(本题满分12分)已知直线与抛物线相交于A,B两点,M是线段AB的中点,过M作轴的垂线交于点N.(1)证明:抛物线在点N处的切线与AB平行;(2)是否存在实数使?若存在,求的值;若不存在,说明理由.21.(本题满分12分)已知函数(1)讨论的单调性;(2)设,若对,,求的取值范围.请考生在第22、23两题中任选一题作答,如果两题都做,则按照所做的第一题给分;作答时,请用2B铅笔将答题卡上相应的题号涂黑。...