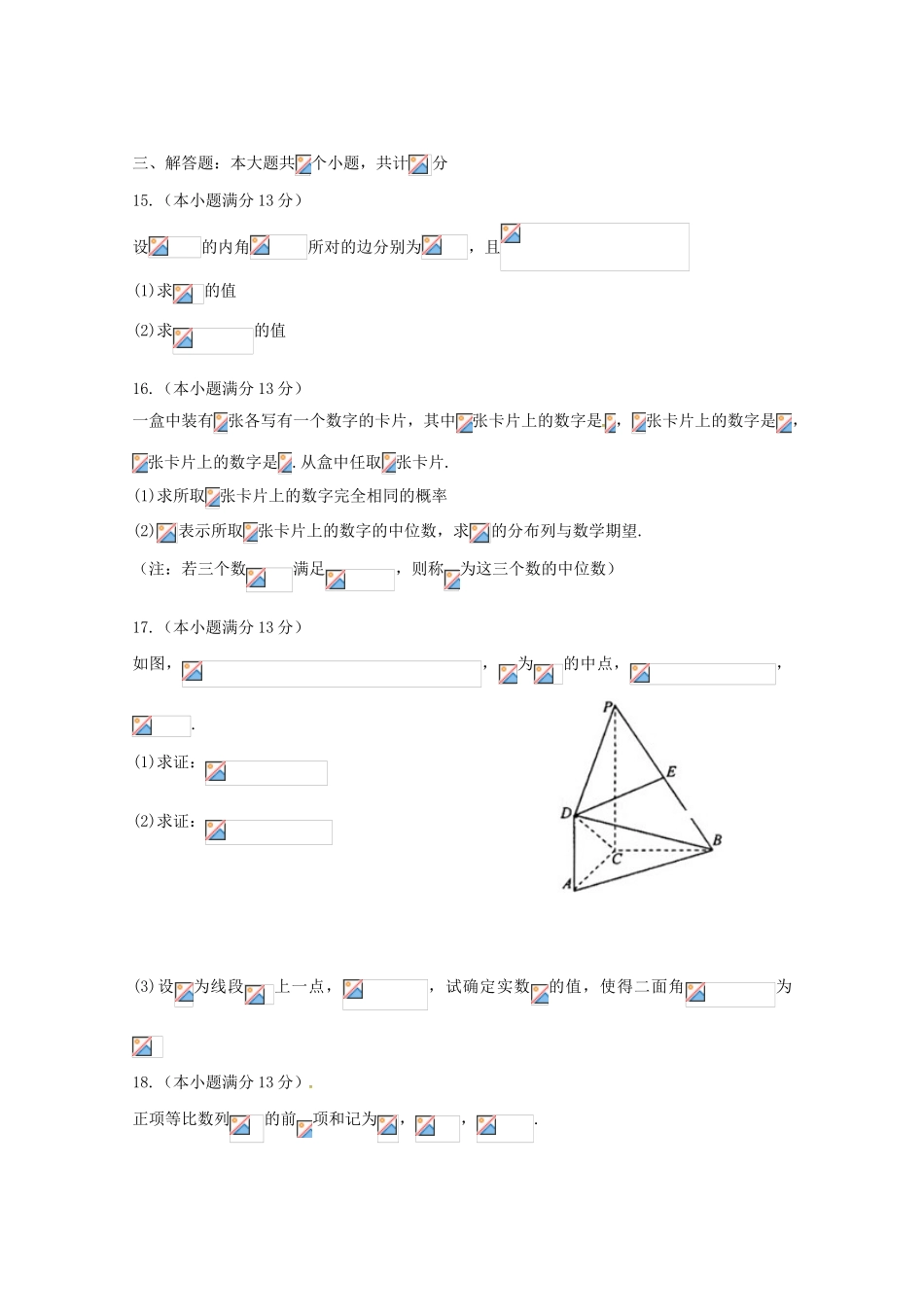
天津市2018届高三数学上学期第一次月考试题理一、选择题:本大题共小题,每小题分,共分1.已知是虚数单位,则复数2.设变量满足约束条件,则目标函数的最小值是3.阅读右面的程序框图,则输出的4.在的二项展开式中,的系数为5.已知,那么是的6.已知双曲线的右焦点与抛物线的焦点重合,则该双曲线的离心率为7.已知定义在上的函数(为实数)为偶函数,记,,,则的大小关系为8.已知函数,若方程恰有四个不同的解,则的取值范围是二、填空题:本大题共小题,每小题分,共分9.设集合,,若,则实数10.设数列是首相为,公差为的等差数列,为其前项和.若成等比数列,则的值为11.直角坐标系中,以原点为极点,轴的正半轴为极轴建立极坐标系,设点分别在曲线(为参数)和曲线上,则的最小值为12.函数的最小值为13.已知棱长为的正四面体的各顶点均在同一球面上,则该球的体积为14.梯形中,,点在线段上,点在线段上,且,则的最小值为三、解答题:本大题共个小题,共计分15.(本小题满分13分)设的内角所对的边分别为,且(1)求的值(2)求的值16.(本小题满分13分)一盒中装有张各写有一个数字的卡片,其中张卡片上的数字是,张卡片上的数字是,张卡片上的数字是.从盒中任取张卡片.(1)求所取张卡片上的数字完全相同的概率(2)表示所取张卡片上的数字的中位数,求的分布列与数学期望.(注:若三个数满足,则称为这三个数的中位数)17.(本小题满分13分)如图,,为的中点,,.(1)求证:(2)求证:(3)设为线段上一点,,试确定实数的值,使得二面角为18.(本小题满分13分)正项等比数列的前项和记为,,.(1)求数列的通项公式(2)等差数列的各项为正,且,又成等比数列,设,求数列的前项和.19.(本小题满分14分)已知椭圆经过点,离心率为,左右焦点分别为.(1)求椭圆的方程(2)若直线与椭圆交于两点,与以为直径的圆交于两点,且满足,求直线的方程.20.(本小题满分14分)已知函数的最小值为,其中.(1)求的值(2)若对任意的,有成立,求实数的最小值(3)证明:天津市耀华中学2018届高三年级暑假验收考试数学参考答案(理科)一、选择题:本大题共小题,每小题分,共分1.A;2.C;3.B;4.C;5.B;6.D;7.A;8.B二、填空题:本大题共小题,每小题分,共分9.;10.;11.3;12.;13.;14.三、解答题:本大题共个小题,共计分15.(本小题满分13分)解:(1)由与余弦定理得,,又,解得(2)又,,与正弦定理得,,.所以16.(本小题满分13分)解:(1)由古典概型中的概率计算公式知所求概率为(2)的所有可能值为1,2,3,且,,,故的分布列为:123从而17.(本小题满分13分)(1)证明:以C为原点建立空间直角坐标系,,,则,,易知为平面ABC的一个法向量,,;(2)证明:,,,,,,;(3)解:由(2)知平面BCD的法向量为,,,而,设平面QCD的法向量为,由得,,令,则,,即,故,解得,由得,.18.(本小题满分13分)解:(1)设公比为,则,得,,;(2)设的公差为,由,可设,又,,,由题意可得,解得,等差数列的各项为正,,,;,则,①,②由①-②得,,.19.(本小题满分14分)解:(1)由题设,,,解得椭圆的方程为;(2)由题设,以,为直径的圆的方程为,圆心到直线的距离为由得,①,,设,,由得,,,,,由得,,解得,满足①,∴直线的方程为.20.(本小题满分14分)解:(1)的定义域为,由,得当时,,函数单调递减;当时,,函数单调递增,为唯一的极小值,也是最小值,故由题意,所以.(2)当时,取,有,故不符合题意当时,令,即令,得,①当时,,在上恒成立,因此在上单调递减,从而对于任意的,总有,即在上恒成立,故符合题意.②当时,,对于,故在内单调递增,因此,当取时,,即不成立.故不符合题意.(3)证明:当时,不等式左边右边,所以不等式成立,当时,在(2)中取得,,从而所以综上.