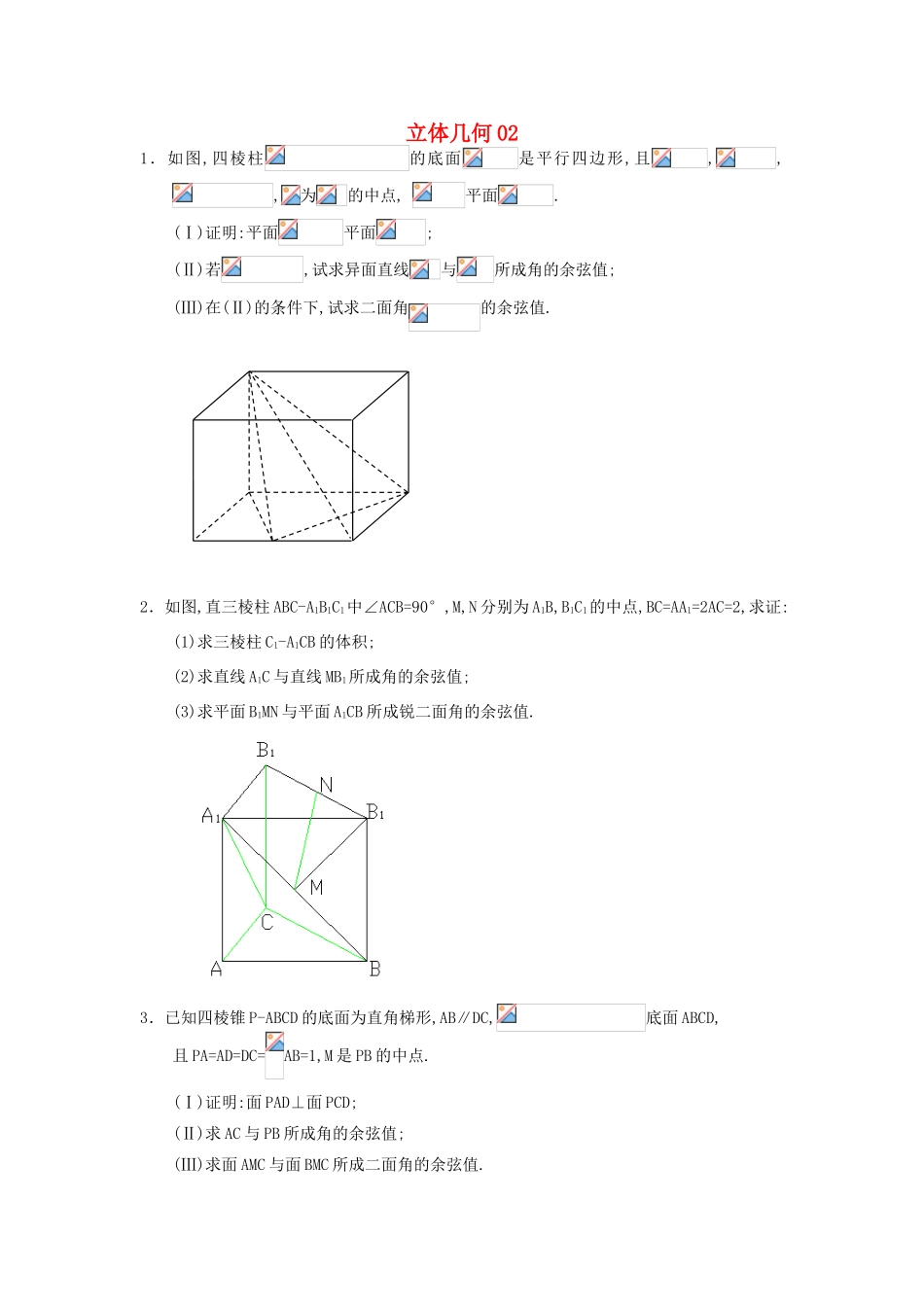
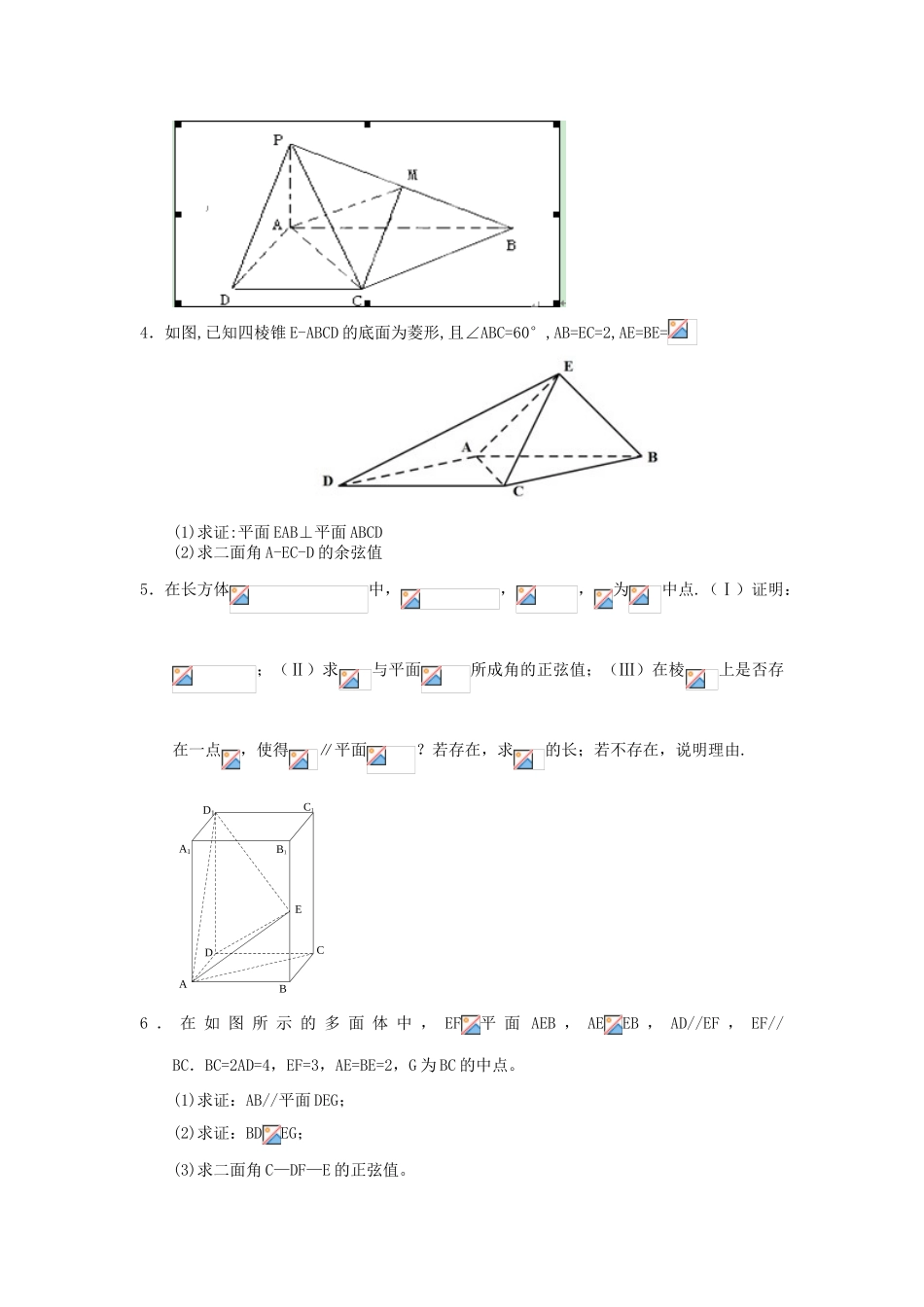
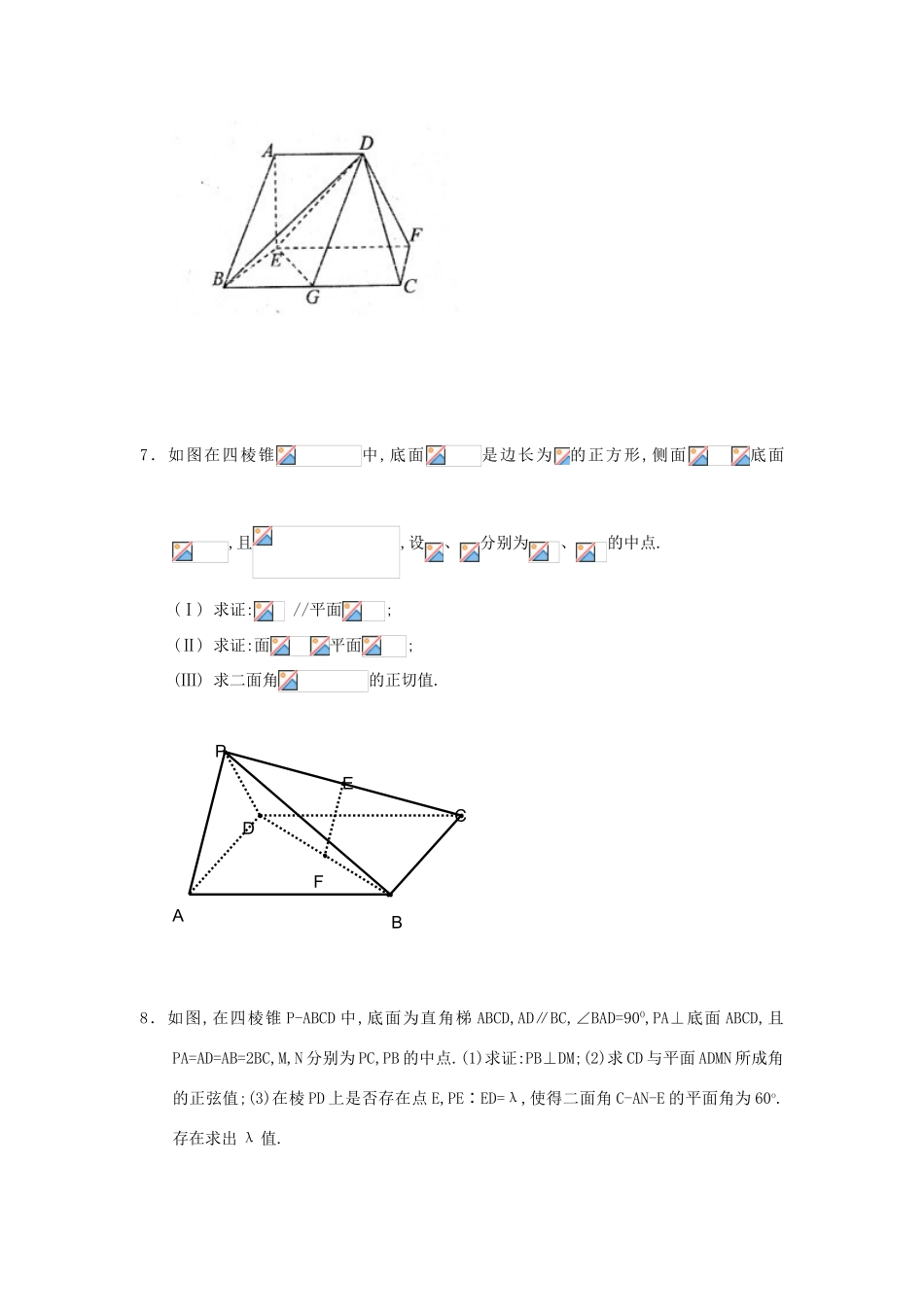
立体几何021.如图,四棱柱的底面是平行四边形,且,,,为的中点,平面.(Ⅰ)证明:平面平面;(Ⅱ)若,试求异面直线与所成角的余弦值;(Ⅲ)在(Ⅱ)的条件下,试求二面角的余弦值.2.如图,直三棱柱ABC-A1B1C1中∠ACB=90°,M,N分别为A1B,B1C1的中点,BC=AA1=2AC=2,求证:(1)求三棱柱C1-A1CB的体积;(2)求直线A1C与直线MB1所成角的余弦值;(3)求平面B1MN与平面A1CB所成锐二面角的余弦值.3.已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,底面ABCD,且PA=AD=DC=AB=1,M是PB的中点.(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值.4.如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=(1)求证:平面EAB⊥平面ABCD(2)求二面角A-EC-D的余弦值5.在长方体中,,,为中点.(Ⅰ)证明:;(Ⅱ)求与平面所成角的正弦值;(Ⅲ)在棱上是否存在一点,使得∥平面?若存在,求的长;若不存在,说明理由.D1C1B1A1EDCBA6.在如图所示的多面体中,EF平面AEB,AEEB,AD//EF,EF//BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点。(1)求证:AB//平面DEG;(2)求证:BDEG;(3)求二面角C—DF—E的正弦值。7.如图在四棱锥中,底面是边长为的正方形,侧面底面,且,设、分别为、的中点.(Ⅰ)求证://平面;(Ⅱ)求证:面平面;(Ⅲ)求二面角的正切值.8.如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90O,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.(1)求证:PB⊥DM;(2)求CD与平面ADMN所成角的正弦值;(3)在棱PD上是否存在点E,PE∶ED=λ,使得二面角C-AN-E的平面角为60o.存在求出λ值.FEDCBAP9.在四棱锥中,底面是直角梯形,∥,∠,,平面⊥平面.(1)求证:⊥平面;(2)求平面和平面所成二面角(小于)的大小;(3)在棱上是否存在点使得∥平面?若存在,求的值;若不存在,请说明理由.答案解(Ⅰ)依题意,所以是正三角形,又所以,因为平面,平面,所以因为,所以平面因为平面,所以平面平面(Ⅱ)取的中点,连接、,连接,则所以是异面直线与所成的角因为,,所以,,所以(Ⅰ)(Ⅱ)解法2:以为原点,过且垂直于的直线为轴,所在直线为轴、所在直线为建立右手系空间直角坐标系设(),则(Ⅰ)设平面的一个法向量为,则,取,则,从而,同理可得平面的一个法向量为,直接计算知,所以平面平面(Ⅱ)由即解得,所以异面直线与所成角的余弦值(Ⅲ)由(Ⅱ)可知,平面的一个法向量为又,设平面的法向量则得设二面角的平面角为,且为锐角则所以二面角的余弦值为解:(1)--------------4(2)------------8(3)------------------13解:(1)证明:取AB的中点O,连接EO,CO△AEB为等腰直角三角形∴EO⊥AB,EO=1又 AB=BC,∠ABC=60°,∴△ABC是等边三角形,,又 EO⊥平面ABCD,又EO平面EAB,∴平面EAB⊥平面ABCD(2)以AB的中点O为坐标原点,OB所在直线为y轴,OE所在直线为z轴,如图建系则,,=(0,2,0)设平面DCE的法向量为,则,即,解得:同理求得平面EAC的一个法向量为,所以二面角A-EC-D的余弦值为(Ⅰ)证明:连接 是长方体,∴平面,又平面∴……1分在长方形中,∴…………2分又∴平面,…………3分而平面∴………4分(Ⅱ)如图建立空间直角坐标系,则,………5分设平面的法向量为,则令,则………7分…………8分zyxD1C1B1A1EDCBA所以与平面所成角的正弦值为………………9分(Ⅲ)假设在棱上存在一点,使得∥平面.设的坐标为,则因为∥平面所以,即,,解得,………………12分所以在棱上存在一点,使得∥平面,此时的长.……13分法一:(Ⅰ)证明:为平行四边形连结,为中点,为中点∴在中//且平面,平面∴(Ⅱ)证明:因为面面平面面为正方形,,平面所以平面∴又,所以是等腰直角三角形,且即,且、面面又面面面(Ⅲ)【解】:设的中点为,连结,,则由(Ⅱ)知面,,面,,是二面角的平面角中,故所求二面角的正切值为法二:如图,取的中点,连结,. ,∴. 侧面底面,,∴,而分别为的中点,∴,又是正方形,故. ,∴,.以为原点,直线为轴建立空间直线坐标系,则有,,,,,. 为的中点,∴(Ⅰ)证明:易知平面的法向量为而,且,∴//平面(Ⅱ)证明: ,∴,∴,从而,又,,∴,而,∴平面平面(Ⅲ)【解】:由(Ⅱ)知平面的法向量为.设平面的法向量为. ,∴由可得,令,则,故∴,即二面角的余弦值为,所以二面角的正切值为解:(1)如图...