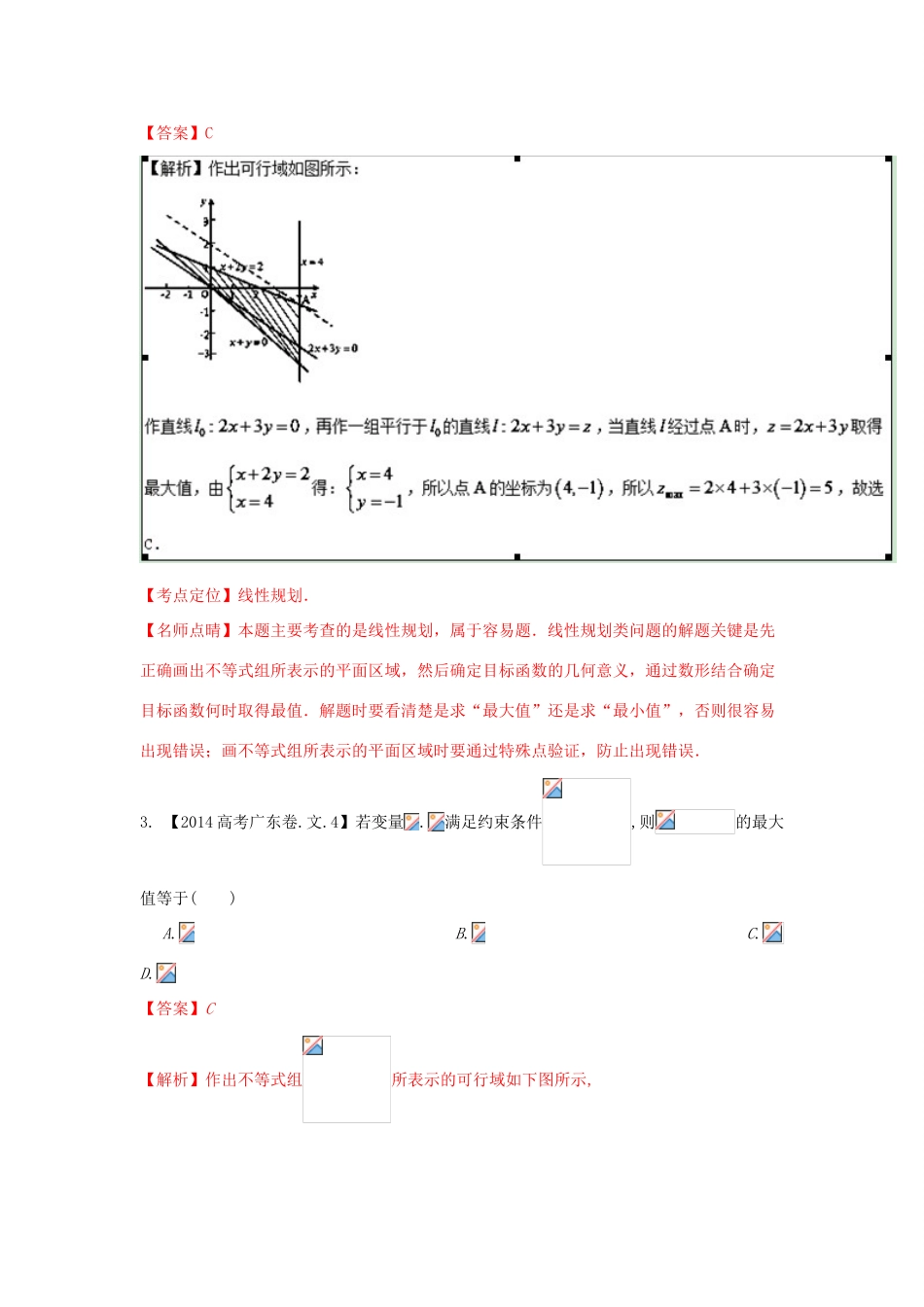
三年高考(2014-2016)数学(文)试题分项版解析第七章不等式一、选择题1.【2016高考山东文数】若变量x,y满足则x2+y2的最大值是()(A)4(B)9(C)10(D)12【答案】C【解析】试题分析:画出可行域如图所示,点到原点距离最大,所以,选C.考点:简单线性规划【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目看,简单线性规划问题,是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间距离等,考查考生的绘图、用图能力,以及应用数学解决实际问题的能力.2.【2015高考广东,文4】若变量,满足约束条件,则的最大值为()A.B.C.D.【答案】C【考点定位】线性规划.【名师点晴】本题主要考查的是线性规划,属于容易题.线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域,然后确定目标函数的几何意义,通过数形结合确定目标函数何时取得最值.解题时要看清楚是求“最大值”还是求“最小值”,否则很容易出现错误;画不等式组所表示的平面区域时要通过特殊点验证,防止出现错误.3.【2014高考广东卷.文.4】若变量.满足约束条件,则的最大值等于()A.B.C.D.【答案】C【解析】作出不等式组所表示的可行域如下图所示,xOyAl:z=2x+yy=3x=4x+2y=8直线交直线于点,作直线,则为直线在轴上的截距,当直线经过可行域上的点时,直线在轴上的截距最大,此时取最大值,即,故选C.【考点定位】本题考查线性规划中线性目标函数的最值,属于中等题.【名师点晴】本题主要考查的是线性规划,属于中等题.线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域,然后确定目标函数的几何意义,通过数形结合确定目标函数何时取得最值.解题时要看清楚是求“最大值”还是求“最小值”,否则很容易出现错误;画不等式组所表示的平面区域时要通过特殊点验证,防止出现错误.4.【2015高考湖南,文7】若实数满足,则的最小值为()A、B、2C、2D、4【答案】C【解析】(当且仅当时取等号),所以的最小值为,故选C.【考点定位】基本不等式【名师点睛】基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,因此可以用在一些不等式的证明中,还可以用于求代数式的最值或取值范围.如果条件等式中,同时含有两个变量的和与积的形式,就可以直接利用基本不等式对两个正数的和与积进行转化,然后通过解不等式进行求解.5.【2015高考湖南,文4】若变量满足约束条件,则的最小值为()A、B、0C、1D、2【答案】A【解析】由约束条作出可行域如图,由图可知,最优解为A,联立,∴在点A处取得最小值为.故选:A.【考点定位】简单的线性规划【名师点睛】求目标函数的最值的一般步骤为:一画二移三求.其关键是准确作出可行域理解目标函数的意义.常见的目标函数有:(1)截距型:形如,求这类目标函数的最值常将函数转化为直线的斜截式:,通过求直线的截距的最值间接求出的最值.(2)距离型:形如.(3)斜率型:形如.注意:转化的等价性及几何意义.6.【2014山东.文10】已知满足约束条件,当目标函数在该约束条件下取到最小值时,的最小值为()A.5B.4C.D.2【答案】考点:简单线性规划的应用,二次函数的图象和性质.【名师点睛】本题考查简单线性规划、二次函数的图象和性质.此类问题的基本解法是“图表法”,即通过画可行域及直线ax+by=0,平移直线ax+by=0,观察其在y轴的纵截距变化情况,得出最优解,得到a,b的关系.要注意y的系数正负不同时,结论恰好相反.本题属于小综合题,由以往单纯考查线性规划问题,转变成此类题,增大了解题的难度,也给人耳目一新的感觉.7.【2016高考浙江文数】若平面区域夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是()A.B.C.D.【答案】B【解析】试题分析:画出不等式组的平面区域如题所示,由得,由得,由题意可知,当斜率为1的两条直线分别过点A和点B时,两直线的距离最小,即.故选B.考点:线性规划.【思路点睛】先根据不等式组画出可行域,再根据可行域的特点确定取得最值的最优解,代入计算.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.8.【2015高...