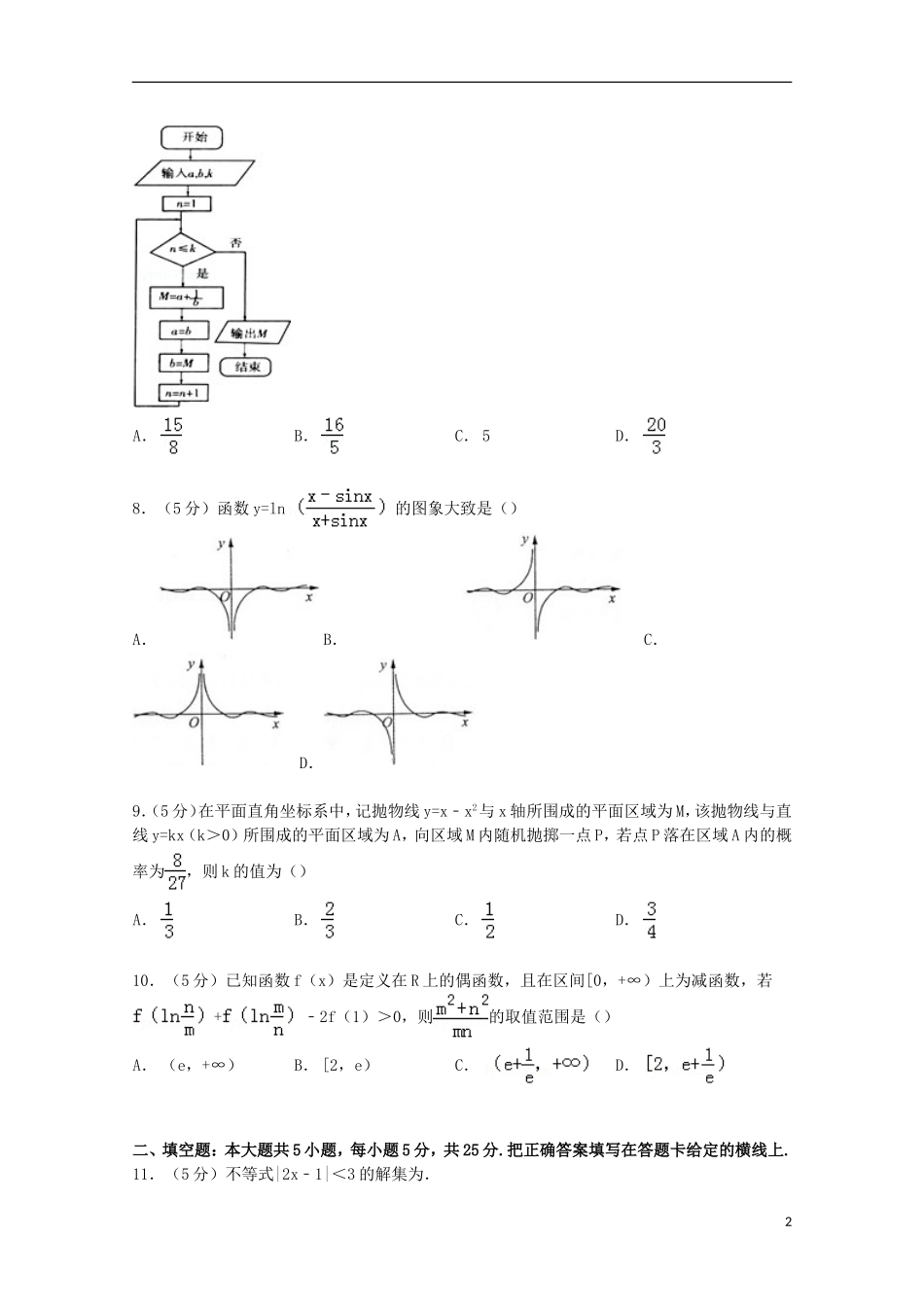
山东省临沂市2015届高考数学模拟试卷(理科)(5月份)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)复数z=1﹣i,则对应的点所在象限为()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)设集合A={x|x2﹣3x+2=0},则满足A∪B={0,1,2}的集合B的个数是()A.1B.3C.4D.63.(5分)某市对汽车限购政策进行了调查,在参加调查的300名有车人中116名持反对意见,200名无车人中有121名持反对意见,在运用这些数据说明“拥有车辆”与“反对汽车限购政策”是否有关系时,最有说服力的方法是()A.平均数与方差B.回归直线方程C.独立性检验D.概率4.(5分)下列函数中,与函数y=的奇偶性相同,且在(﹣∞,0)上单调性也相同的是()A.B.y=x2+2C.y=x3﹣3D.5.(5分)将函数y=3sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递减B.在区间[,]上单调递增C.在区间[﹣,]上单调递减D.在区间[﹣,]上单调递增6.(5分)“a=1”是“直线y=x与函数y=ln(x+a)的图象有且仅有一个交点”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)执行如图所示的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=()1A.B.C.5D.8.(5分)函数y=ln的图象大致是()A.B.C.D.9.(5分)在平面直角坐标系中,记抛物线y=x﹣x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为A,向区域M内随机抛掷一点P,若点P落在区域A内的概率为,则k的值为()A.B.C.D.10.(5分)已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上为减函数,若+﹣2f(1)>0,则的取值范围是()A.(e,+∞)B.[2,e)C.D.二、填空题:本大题共5小题,每小题5分,共25分.把正确答案填写在答题卡给定的横线上.11.(5分)不等式|2x﹣1|<3的解集为.212.(5分)若cosα=,则sin.13.(5分)若变量x,y满足约束条件且z=2x+y的最小值为﹣3,则k=.14.(5分)某几何体的三视图如图,其侧视图是一个边长为1的等边三角形,俯视图是由两个等边三角形拼成,则该几何体的体积为.15.(5分)如图展示了一个由区间(0,1)到实数集R的映射过程;区间(0,1)中的实数x对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A,B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图③.图③中直线AM与x轴交于点N(n,0),则x的象就是n,记作f(x)=n.下列说法中正确的序号是.(填上所有正确命题的序号)①f(x)在定义域上单调递增;②f(x)的图象关于y轴对称;③是f(x)的零点;④;⑤f(x)>1的解集是.三、解答题:本大题共6小题,共75分,解答应写出必要的文字说明,证明过程或演算步骤.16.(12分)已知向量=(sinA,sinB),=(cosB,cosA),•=sin2C,且A,B,C分别为△ABC的三边a,b,c所对的角.3(I)求角C的大小;(Ⅱ)若sinA,sinC,sinB成等差数列,且△ABC的面积为,求c边的长.17.(12分)如图,在四棱锥P﹣ABCD中,AB∥CD,PA⊥AD,CD⊥AD,PA=AD=CD=2AB,E,F分别为PC,CD的中点,DE=EC.(Ⅰ)求证:平面ABE⊥平面BEF;(Ⅱ)求锐二面角E﹣BD﹣C的余弦值.18.(12分)在某学校组织的一次利于定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:ξ02345Pp1p2p3p4(I)求q2的值;(Ⅱ)求随机变量ξ的数学期望.19.(12分)已知公差不为0的等差数列{an}的前n项和Sn,S5=25,且a2,a5,a14成等比数列.(I)求数列{an}的通项公式;(Ⅱ)设bn=,求证:Tn≥.20.(13分)已知椭圆C:+=1(a>b>0)的上顶点为(0,1),且离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)证明:过椭圆C1:+=1(m>n>0)上一点Q(x0,y0)的...