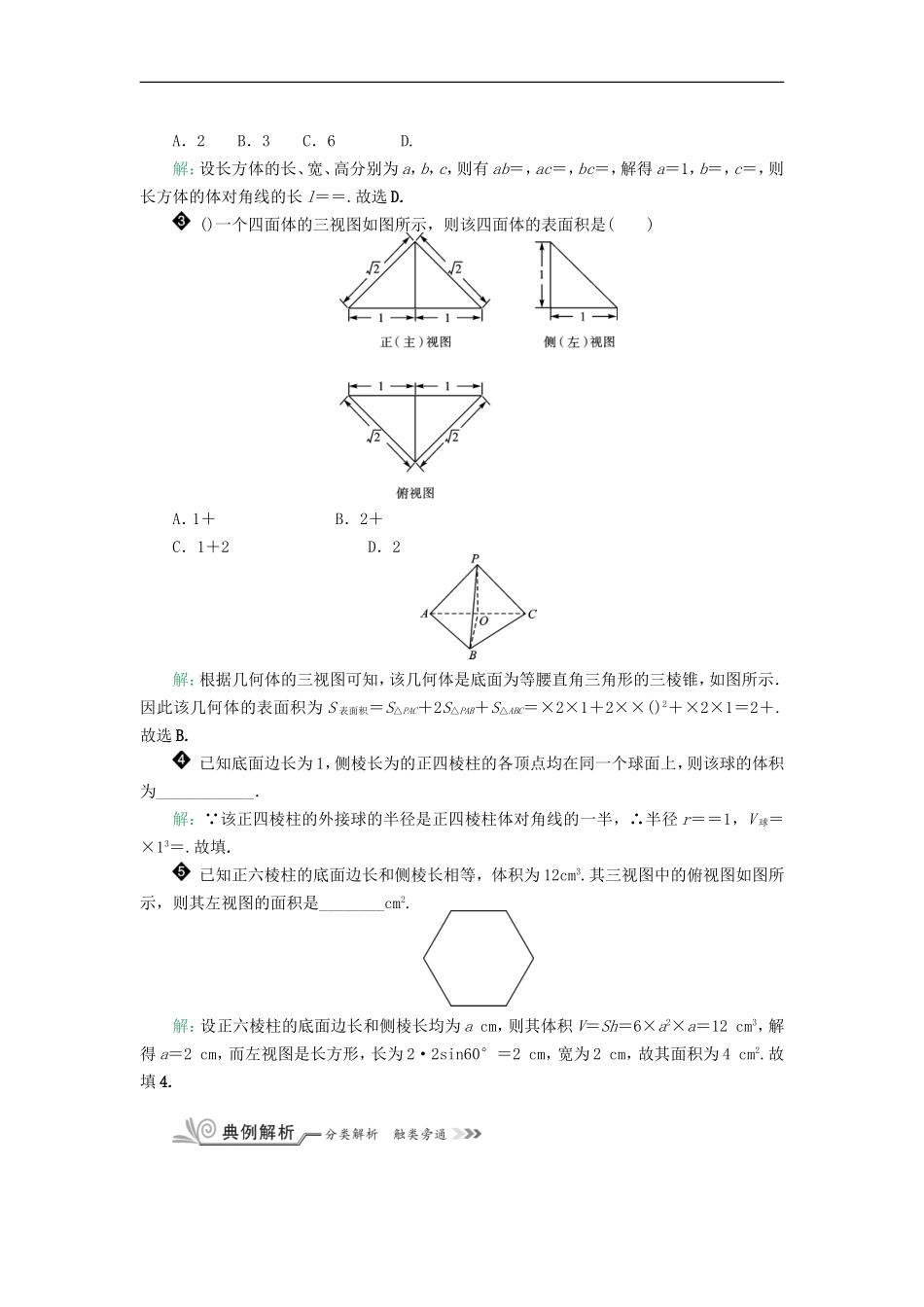
§8.2空间几何体的表面积与体积1.柱体、锥体、台体的表面积(1)直棱柱、正棱锥、正棱台的侧面积S直棱柱侧=__________,S正棱锥侧=__________,S正棱台侧=__________(其中C,C′为底面周长,h为高,h′为斜高).(2)圆柱、圆锥、圆台的侧面积S圆柱侧=________,S圆锥侧=________,S圆台侧=________(其中r,r′为底面半径,l为母线长).(3)柱或台的表面积等于________与__________的和,锥体的表面积等于________与__________的和.2.柱体、锥体、台体的体积(1)棱柱、棱锥、棱台的体积V棱柱=__________,V棱锥=__________,V棱台=__________(其中S,S′为底面积,h为高).(2)圆柱、圆锥、圆台的体积V圆柱=__________,V圆锥=__________,V圆台=__________(其中r,r′为底面圆的半径,h为高).3.球的表面积与体积(1)半径为R的球的表面积S球=________.(2)半径为R的球的体积V球=________.自查自纠1.(1)ChCh′h′(2)2πrlπrlπ(r+r′)l(3)侧面积两个底面积侧面积一个底面积2.(1)ShShh(2)πr2hπr2hπh3.(1)4πR2(2)πR3已知圆锥的正视图是边长为2的等边三角形,则该圆锥体积为()A.B.πC.D.π解:易知圆锥的底面直径为2,母线长为2,则该圆锥的高为=,因此其体积是π·12×=.故选C.一个长方体共一顶点的三个面的面积分别是,,,则这个长方体的体对角线的长是()A.2B.3C.6D.解:设长方体的长、宽、高分别为a,b,c,则有ab=,ac=,bc=,解得a=1,b=,c=,则长方体的体对角线的长l==.故选D.()一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.2+C.1+2D.2解:根据几何体的三视图可知,该几何体是底面为等腰直角三角形的三棱锥,如图所示.因此该几何体的表面积为S表面积=S△PAC+2S△PAB+S△ABC=×2×1+2××()2+×2×1=2+.故选B.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为____________.解: 该正四棱柱的外接球的半径是正四棱柱体对角线的一半,∴半径r==1,V球=×13=.故填.已知正六棱柱的底面边长和侧棱长相等,体积为12cm3.其三视图中的俯视图如图所示,则其左视图的面积是________cm2.解:设正六棱柱的底面边长和侧棱长均为acm,则其体积V=Sh=6×a2×a=12cm3,解得a=2cm,而左视图是长方形,长为2·2sin60°=2cm,宽为2cm,故其面积为4cm2.故填4.类型一空间几何体的面积问题如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC边上的高,沿AD把△ABD折起,使∠BDC=90°.若BD=1,求三棱锥DABC的表面积.解: 折起前AD是BC边上的高,∴沿AD把△ABD折起后,AD⊥DC,AD⊥BD.又∠BDC=90°,DB=DA=DC=1,∴AB=BC=CA=.从而S△DAB=S△DBC=S△DCA=×1×1=,S△ABC=×××sin60°=.∴三棱锥DABC的表面积S=×3+=.【点拨】充分运用图形在翻折前后的不变性,如角的大小不变,线段长度不变等.()某三棱锥的三视图如图所示,则该三棱锥的表面积是()A.2+B.4+C.2+2D.5解:由三视图作出该几何体的直观图如图所示,底面△ABC是等腰三角形,PC⊥平面ABC,取AB的中点D,连接CD,PD,易证AB⊥PD,由三视图中的数据知PC=1,AB=CD=2,∴AC=BC=,PD=,∴S△ABC=×2×2=2,S△PAC=S△PBC=××1=,S△PAB=×2×=,∴S表=2+2.故选C.类型二空间旋转体的面积问题如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.解:如图,设球的一条半径与圆柱相应的母线的夹角为α,圆柱侧面积S=2π×4sinα×2×4cosα=32πsin2α,当α=时,S取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.故填32π.【点拨】根据球的性质,内接圆柱上、下底面中心连线的中点为球心,且圆柱的上、下底面圆周均在球面上,球心和圆柱的上、下底面圆上的点的连线与母线的夹角相等,这些为我们建立圆柱的侧面积与上述夹角之间的函数关系提供了依据.()一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4解:该几何体为半圆柱,底面半径为1,高为2,其表面积为π×12+2×2+×2π×1×2=3π+4.故...