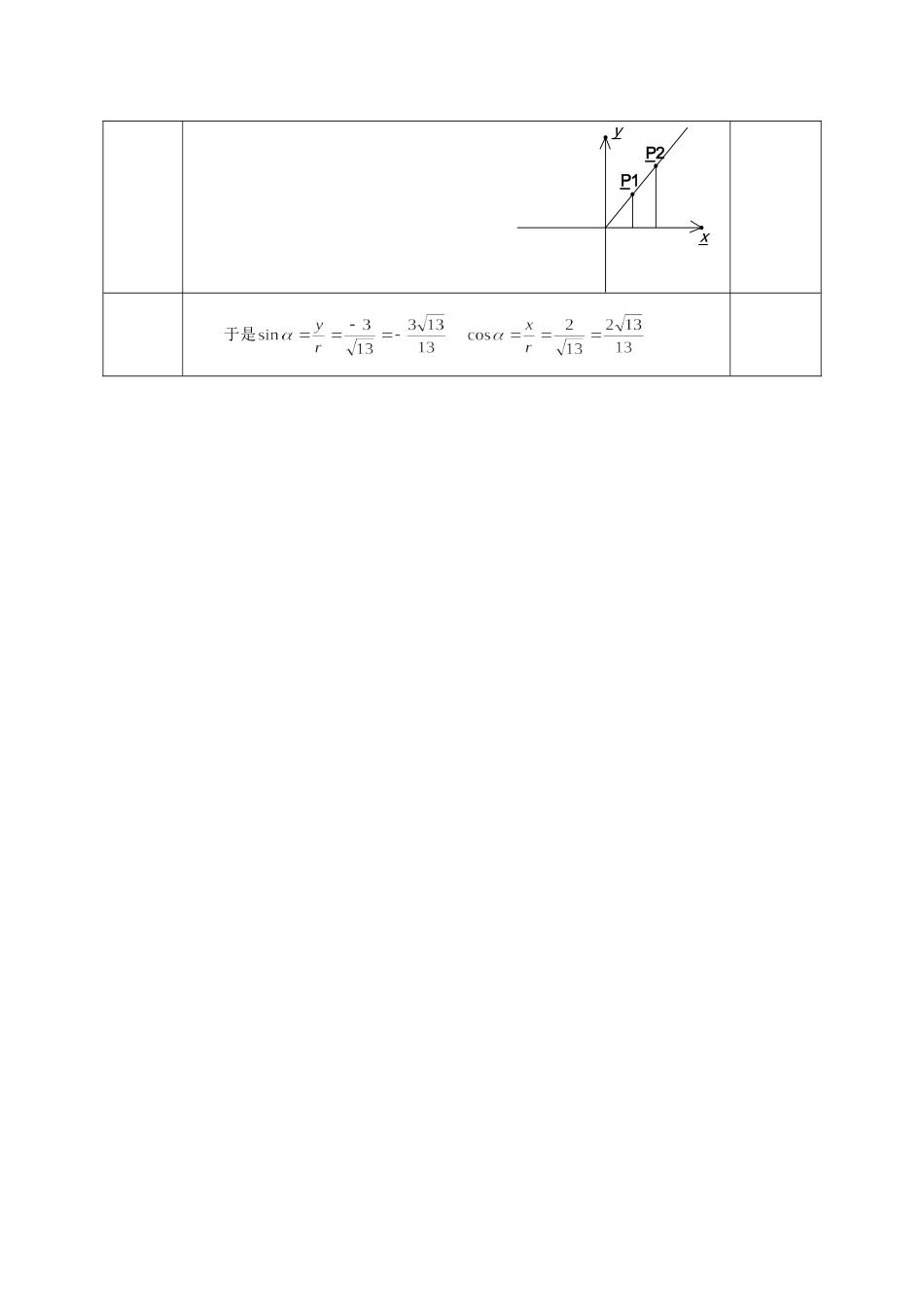
4-1.2.1任意角的三角函数(一)【课题】:任意角的三角函数定义方案一:【设计与执教者】:广州市第六中学,莫秀玲,supermoxiuling@126.com【教学时间】:2007年3月【学情分析】:(适用于平行班)教学对象是高一的学生,学生在初中已经学习了锐角三角函数的有关知识。本节课,学生是在此基础上结合刚学习的任意角及弧度制知识,进一步学习任意角的三角函数知识。我们通过对三角函数定义的剖析,使学生理解从锐角三角函数到任意角三角函数中定义的变化,认识锐角三角函数是任意角三角函数的一种特例,加深特殊与一般关系的理解,从而掌握任意角的三角函数定义,这在平行班教学中是可行的。【教学目标】:(1)理解并掌握任意角三角函数的定义;(2)理解并掌握各种三角函数在各象限内的符号;(3)理解并掌握终边相同的角的同一三角函数值相等.【教学重点】:理解并掌握任意角三角函数的定义;理解并掌握各种三角函数在各象限内的符号;理解并掌握终边相同的角的同一三角函数值相等.【教学难点】:理解并掌握任意角三角函数的定义.【教学突破点】:借助平面直角坐标系,通过对三角函数定义的剖析,使学生理解从锐角三角函数到任意角三角函数中定义的变化,认识锐角三角函数是任意角三角函数的一种特例,加深特殊与一般关系的理解,达到突破难点之目的.【教法、学法设计】:采用观察法、对比法和定义法。通过图示,使学生观察三角函数定义的变化:从锐角三角函数到任意角三角函数,由边的比变为坐标与距离、坐标与坐标的比,在理解掌握定义的基础上,通过对比,认识锐角三角函数是任意角三角函数的一种特例,加深特殊与一般关系的理解。通过对定义的剖析,使学生对各种三角函数在各象限内的符号,以及终边相同的角的同一三角函数值相等有比较深刻的认识.【课前准备】:课件【教学过程设计】:教学环节教学活动设计意图一、复习引入1.同学们还记得我们在初中学习过的锐角三角函数吗?看图试填空:2.前面我们对角的概念进行了扩充,并学习了弧度制,知道角的集合与实数集是一一对应的,在这个基础上,今天我们来研究任意角的三角函数.温故知新cbaABC二、探究新知对于锐角三角函数,我们是在直角三角形中定义的,今天,对于任意角的三角函数,我们利用平面直角坐标系来进行研究.1.任意角的三角函数定义设是一个任意角,在的终边上任取(异于原点的)一点P(x,y)则P与原点的距离.比值叫做的正弦,记作:.比值叫做的余弦,记作:.比值叫做的正切,记作:.学生活动:学生阅读教材,自学有关概念.教师引导:对比锐角三角函数的定义,任意角三角函数的定义有何变化?学生活动:独立思考后,分小组讨论.教师进一步引导学生:从锐角三角函数到任意角三角函数,由边的比变为什么与什么的比?教师引导学生回答并归纳出:从锐角三角函数到任意角三角函数,由边的比变为坐标与距离、坐标与坐标的比.教师引导:锐角三角函数与任意角三角函数之间有何联系?谁是谁的特殊情形?学生讨论归纳:锐角三角函数是任意角三角函数的特殊情形.教师引导:上述四个比值会不会随点P在的终边上的位置的改变而改变呢?(教师画图示意,引导学生思考)学生活动:分小组讨论,并举手回答.教师归纳:根据相似三角形的知识,对于终边不在坐标轴上确定的角,上述四个比值都不会随P点在的终边上的位置的改变而改变.即对于确定的角,上面的四个比值都是唯一确定的实数,这就是说,正弦、余弦、正切都是以角为自变量,以比值为函数值的函数.以上三种函数,统称为三角函数.注意:sin是个整体符号,不能认为是“sin”与“”的积.其余两个符号也是这样.例1已知角的终边经过点P(2,-3)(如右图),求的正弦、余弦、正切值.解: x=2,y=-3∴引导学生阅读教材,培养自学能力引导学生思考,教师归纳,明晰概念学生口答,教师板书,巩固新学习的概念ry)(x,P于是_x_y_P1_P22.终边相同的角的同一三角函数值相等引例分别求出30°和390°的正弦、余弦、正切值.解:sin30°=sin390°=cos30°=cos390°=tan30°=tan390°=学生活动:跃跃欲试,画图计算.教师引导:(1)引导建立平面直角坐标系.(以后我们在平面直角坐标系内研究角的问题,...