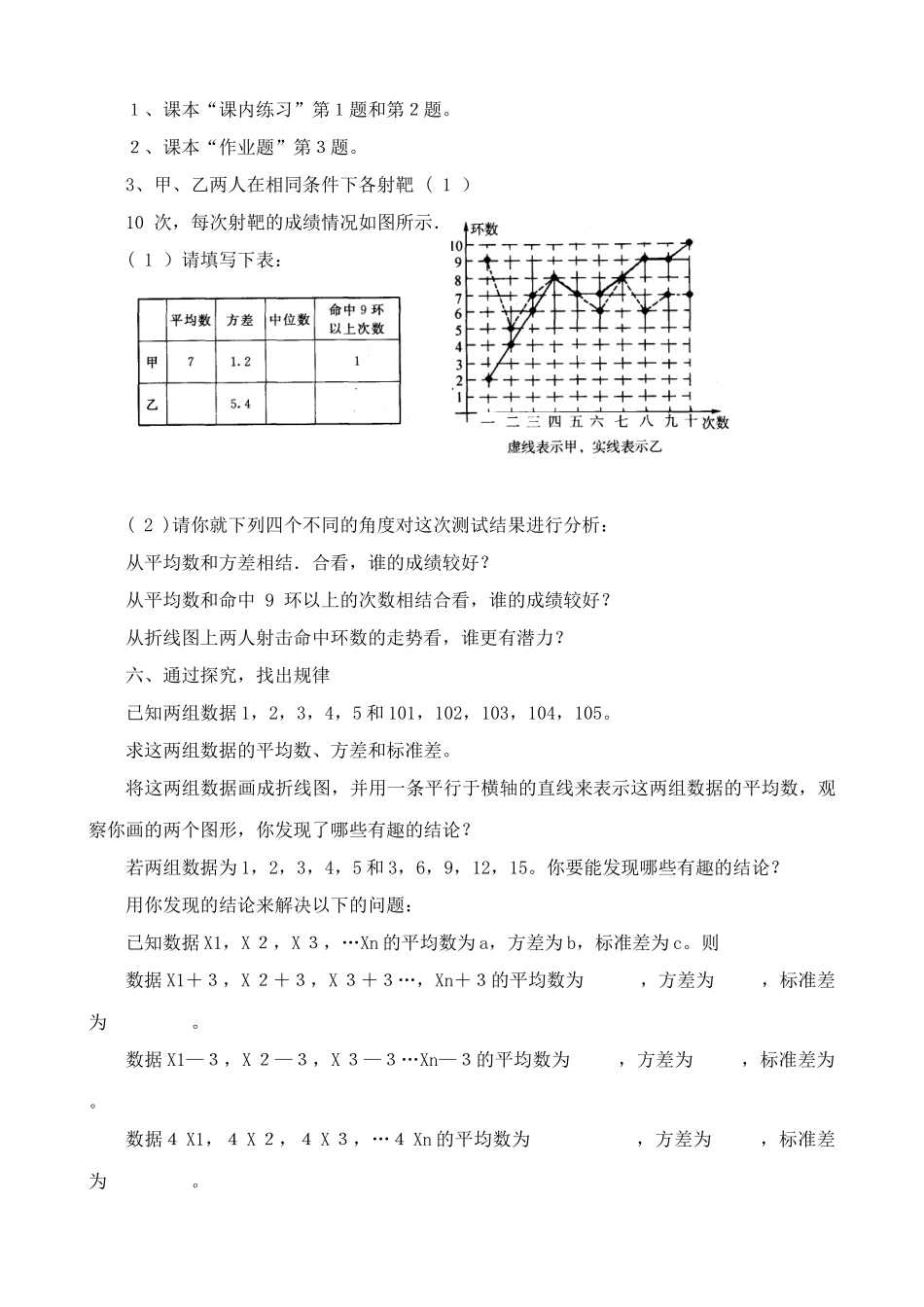
方差和标准差〖教学目标〗◆1、了解方差、标准差的概念.◆2、会求一组数据的方差、标准差,并会用他们表示数据的离散程度.◆3、能用样本的方差来估计总体的方差.◆4、通过实际情景,提出问题,并寻求解决问题的方法,培养学生应用数学的意识和能力.〖教学重点与难点〗◆教学重点:本节教学的重点是方差的概念和计算。.◆教学难点:方差如何表示数据的离散程度,学生不容易理解,是本节教学的难点.〖教学过程〗一、创设情景,提出问题甲、乙两名射击手的测试成绩统计如下表:第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068①请分别算出甲、乙两名射击手的平均成绩;②请根据这两名射击手的成绩在图中画出折线图;二、合作交流,感知问题请根据统计图,思考问题:①、甲、乙两名射击手他们每次射击成绩与他们的平均成绩比较,哪一个偏离程度较低?②、射击成绩偏离平均数的程度与数据的离散程度与折线的波动情况有怎样的联系?③、用怎样的特征数来表示数据的偏离程度?可否用各个数据与平均的差的累计数来表示数据的偏离程度?④、是否可用各个数据与平均数的差的平方和来表示数据的偏离程度?⑤、数据的偏离程度还与什么有关?要比较两组样本容量不相同的数据的偏离平均数的程度,应如何比较?三、概括总结,得出概念根据以上问题情景,在学生讨论,教师补充的基础上得出方差的概念、计算方法、及用方差来判断数据的稳定性。方差的单位和数据的单位不统一,引出标准差的概念。(注意:在比较两组数据特征时,应取相同的样本容量,计算过程可借助计数器)现要挑选一名射击手参加比赛,你认为挑选哪一位比较适宜?为什么?(这个问题没有标准答案,要根据比赛的具体情况来分析,作出结论)四、应用概念,巩固新知已知某样本的方差是4,则这个样本的标准差是。已知一个样本1,3,2,X,5,其平均数是3,则这个样本的标准差是。甲、乙两名战士在射击训练中,打靶的次数相同,且中环的平均数X甲=X乙,如果甲的射击成绩比较稳定,那么方差的大小关系是S2甲S2乙已知一个样本的方差是S=[(X1—4)2+(X2—4)2+…+(X5—4)2],则这个样本的平均数是,样本的容量是。5、八年级(5)班要从黎明和张军两位侯选人中选出一人去参加学科竞赛,他们在平时的5次测试中成绩如下(单位:分)黎明:652653654652654张军:667662653640643如果你是班主任,在收集了上述数据后,你将利用哪些统计的知识来决定这一个名额?(解题步骤:先求平均数,再求方差,然后判断得出结论)五、巩固练习,反馈信息1、课本“课内练习”第1题和第2题。2、课本“作业题”第3题。3、甲、乙两人在相同条件下各射靶(1)10次,每次射靶的成绩情况如图所示.(1)请填写下表:(2)请你就下列四个不同的角度对这次测试结果进行分析:从平均数和方差相结.合看,谁的成绩较好?从平均数和命中9环以上的次数相结合看,谁的成绩较好?从折线图上两人射击命中环数的走势看,谁更有潜力?六、通过探究,找出规律已知两组数据1,2,3,4,5和101,102,103,104,105。求这两组数据的平均数、方差和标准差。将这两组数据画成折线图,并用一条平行于横轴的直线来表示这两组数据的平均数,观察你画的两个图形,你发现了哪些有趣的结论?若两组数据为1,2,3,4,5和3,6,9,12,15。你要能发现哪些有趣的结论?用你发现的结论来解决以下的问题:已知数据X1,X2,X3,…Xn的平均数为a,方差为b,标准差为c。则数据X1+3,X2+3,X3+3…,Xn+3的平均数为,方差为,标准差为。数据X1—3,X2—3,X3—3…Xn—3的平均数为,方差为,标准差为。数据4X1,4X2,4X3,…4Xn的平均数为,方差为,标准差为。数据2X1—3,2X2—3,2X3—3,…2Xn—3的平均数为,方差为,标准差为。小结回顾,反思提高这节课我们学习了方差、标准差的概念,方差的实质是各数据与平均数的差的平方的平均数。方差越大,说明数据的波动越大,越不稳定。标准差是方差的一个派生概念,它的优点是单位和样本的数据单位保持一致,给计算和研究带来方便。利用方差比较数据波动大小的方法和步骤:先求平均数,再...