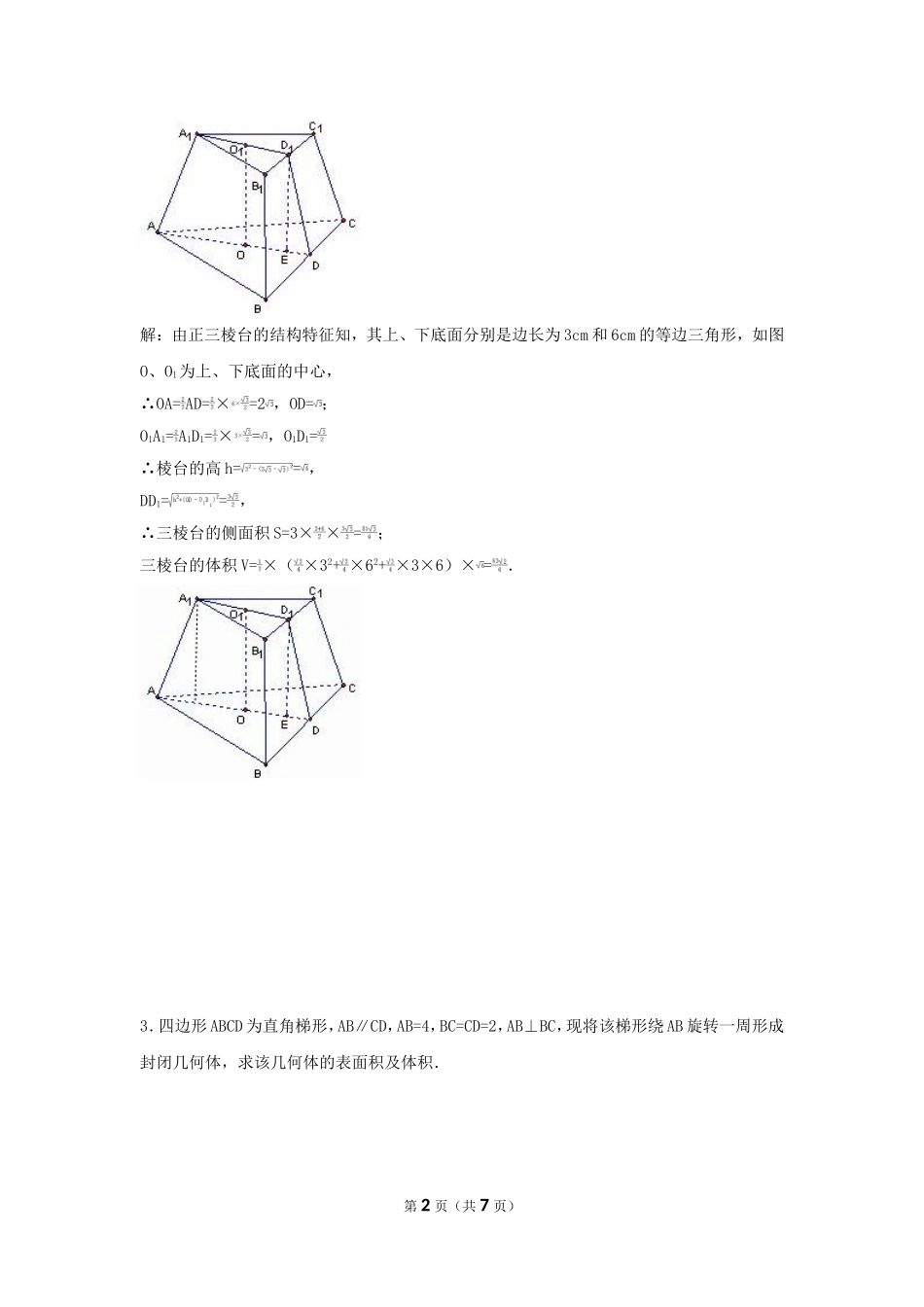
几何体的表面积和体积解答基础1.如图,在底半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积和圆锥的体积.解:圆锥的高,圆柱的底面半径r=1,表面积:圆锥体积:=.2.如图,在正三棱台ABC﹣A1B1C1中,已知其上、下底面边长分别为3cm和6cm,AA1=3cm,求此三棱台的侧面积和体积.第1页(共7页)解:由正三棱台的结构特征知,其上、下底面分别是边长为3cm和6cm的等边三角形,如图O、O1为上、下底面的中心,∴OA=AD=×=2,OD=;O1A1=A1D1=×=,O1D1=∴棱台的高h==,DD1==,∴三棱台的侧面积S=3××=;三棱台的体积V=×(×32+×62+×3×6)×=.3.四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB旋转一周形成封闭几何体,求该几何体的表面积及体积.第2页(共7页)解:依题旋转后形成的几何体为上部为圆锥,下部为圆柱的图形,如下图所示:其表面积S=圆锥侧面积+圆柱侧面积+圆柱底面积;∴S=4+8π+4π=12π+4;其体积V=圆锥体积+圆柱体积;∴V=.4.如图,在底面半径为2、母线长为4的圆锥中挖去一个高为的内接圆柱;(1)求圆柱的表面积;(2)求圆锥挖去圆柱剩下几何体的体积.第3页(共7页)解:设圆锥、圆柱的底面半径分别为R、r,高分别为h、h′.(1)圆锥的高h==2,又∵h′=,∴h′=h.∴=,∴r=1.∴S表面积=2S底+S侧=2πr2+2πrh′=2π+2π×=2(1+)π(2)所求体积=5.已知正四棱锥(底面是正方形,顶点在底面的射影是底面的中心)的底面边长为a,侧棱长为a(1)求它的外接球的体积(2)求他的内切球的表面积.解:(1)由题意,四棱锥为正四棱锥,∵该四棱锥的侧棱长为a,底面是边长为a的正方形,∴四棱锥的高为a,第4页(共7页)设外接球的半径为R,则有R2=(a)2+(a﹣R)2,∴R=a,∴外接球的体积为=;(2)设内切球的半径为r,则∴r=a∴表面积为4πr2=.6.已知正方形的边长为a,求侧面积等于这个正方形的面积,高等于这个正方形边长的直圆柱体的体积.解:设底面半径为r,直圆柱体的高为h因为侧面积等于这个正方形的面积,高等于这个正方形边长所以有底面周长2πr=a,h=a,解得,由公式圆柱体体积V=πr2h=.7.已知某个四面体的棱长均为a,(1)求该四面体外接球的体积;(2)求该四面体内切球的体积.解:(1):∵正四面体的棱长为a,∴此四面体一定可以放在正方体中,第5页(共7页)∴我们可以在正方体中寻找此四面体.如图所示,四面体ABCD满足题意,BC=a,∴正方体的棱长为a,∴此四面体的外接球即为此正方体的外接球,∵外接球的直径=正方体的对角线长,∴外接球的半径为R=•=a,所以,球的体积为π•a3=πa3.(2)设正四面体的内切球的半径为r,由于正四面体的每个面的面积为S=•a•a•sin60°=a2,正四面体的高为h==a,故正四面体的体积为V=Sh=a3.再根据V=4[sr]=4×[•a2•r],可得a3=4×[•a2•r],求得r=a,故四面体内切球的体积V′=π•r3=•a3.8.半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为,求球的表面积和体积.解:设正方形ABCD﹣A'B'C'D'的底面ABCD在半球的底面圆上,如图则球心O为ABCD的中心,连结OA'∵正方体的棱长为,∴A0=A′C′=,可得A'O=,即半球的半径R=3,因此,半球的表面积为;体积V=.第6页(共7页)第7页(共7页)