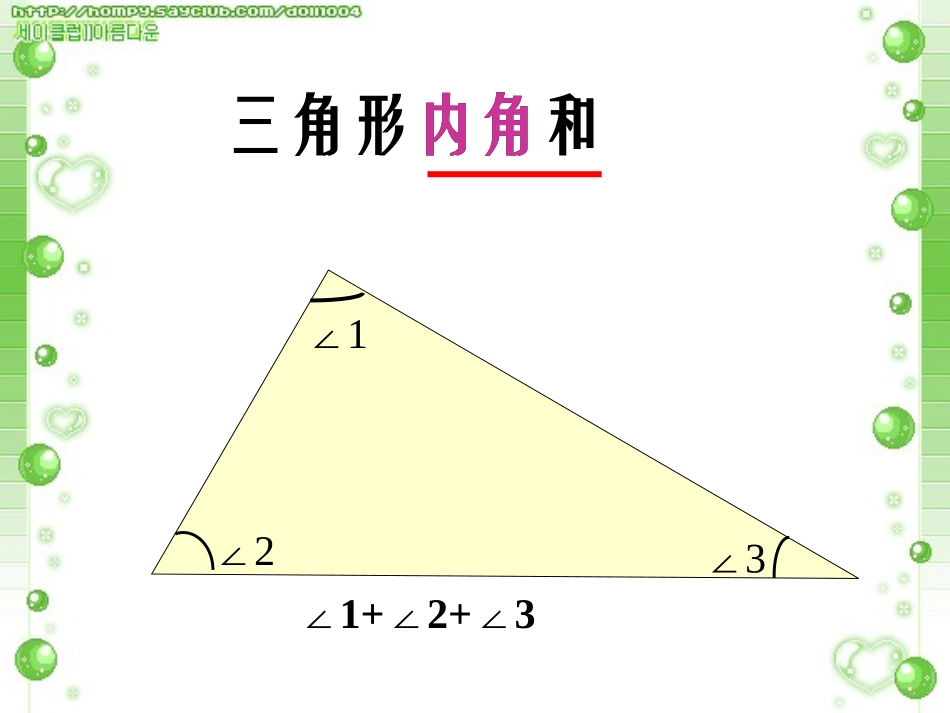
三角形内角和在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”∠1说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”∠2很纳闷。同学们,你们知道其中的道理吗?内角三兄弟之争∠1∠2∠3三角形内角和内角∠1∠2∠3∠1+2+3∠∠90o+60o+30o=180o90o+45o+45o=180o三角形内角和=180°?想一想三角形的三个内角和是180°你有什么办法可以验证它呢?方法一:通过具体的度量,验证三角形的内角和为180°.方法二:剪拼法.把三个角拼在一起试试看?三角形的三个内角和是180°图1图2将三个角撕下来拼成一个平角试一试试一试三角形的内角和等于180°将三个角撕下来拼成一个平角活动三:180°想一想问题:有什么方法可以得到180°1.平角的度数是180°2.两直线平行,同旁内角的和是180°从刚才拼角的过程你能想出证明的方法吗?3.邻补角的和是180°三角形的三个内角和是180°刚才拼角的过程你能想出证明的方法吗刚才拼角的过程你能想出证明的方法吗??图1图2三角形的三个内角和是180°已知:△ABC.求证:∠A+B+C=180°∠∠A.BCB.F21ECBA三角形的内角和等于1800.证明:过A作EFBA∥所以∠B=2∠()同理∠C=1∠()因为∠2+1+BAC=180°∠∠()所以∠B+C+BAC=180°∠∠平角定义两直线平行,内错角相等两直线平行,内错角相等l21EDCBA三角形的内角和等于1800.ABC75o28oABC35oABC45o20o∠A=∠C=∠B=77°55°115°∠A=180°-75°-28°∠A=180°-(75°+28°)∠C=90°-35°闯关练习一60°60°?闯关练习二60°猜一猜,可能是什么三角形?闯关练习三下面三个角哪些能组成三角形?1)60o75o30o2)120o30o40o3)45o45o90o4)35o45o100o√√闯关练习四④三角形中有一个角是60º,那么这个三角形一定是个锐角三角形.()判断下列说法对吗?①钝角三角形的内角和大于锐角三角形的内角和.()②在直角三角形中,两个锐角的和等于90º()③在钝角三角形中,两个锐角的和大于90º()×√××⑤一个三角形中一定不可能有两个钝角。()√闯关练习五两个锐角的和小于90度的三角形是钝角三角形.有两个角的和是90度的三角形是直角三角形一个三角形有1个直角或者至少有两个锐角。例2:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?北ABC北5040DE动动脑:还有其他的解法吗?北北ECBFDA根据题意可知:∠DAC=500,∠DAB=800∠EBC=400ADBE∥解:∠CAB=DAB∠-∠DAC=80°-50°=30°因为ADBE∥所以∠DAB+ABE=180°(∠两直线平行,同旁内角互补)所以∠ABE=180°-∠BAD=180°-80°=100°,所以∠ABC=ABE∠-∠EBC=100°-40°=60°。在△ABC中,∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°答:从C岛看A.B两岛的俯角∠ACB是90°。回顾与小结本节课里你学到了什么???1、三角形内角和的定理:三角形三个内角的和等于180°2、通过思考、去探究、去总结三角形内角和的定理,并且证明方法不止一种。3、探索到一个数学规律,最终还须证明;并且学会怎样有条理的表达。4、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角;5、证明三角形三个内角的和等于180°要转化为:平角等于180°或两直线平行同旁内角和等于180°。小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来的一个角,另一块有原来的两个角。他想重新买一块玻璃安上,小明非常聪明,只带了其中的一块到玻璃店去,就配到了和原来一模一样的玻璃了。你知道他带的是哪一块吗?闯关练习六第1题:求出图中x的值。第2题:如图,从A处观测C处时仰角∠CAD=30º,从B处观测C处时仰角为∠CBD=45º,则∠CBA是度,从C处观测A,B两处时视角∠ACB是度第1题第2题X=X=必要: