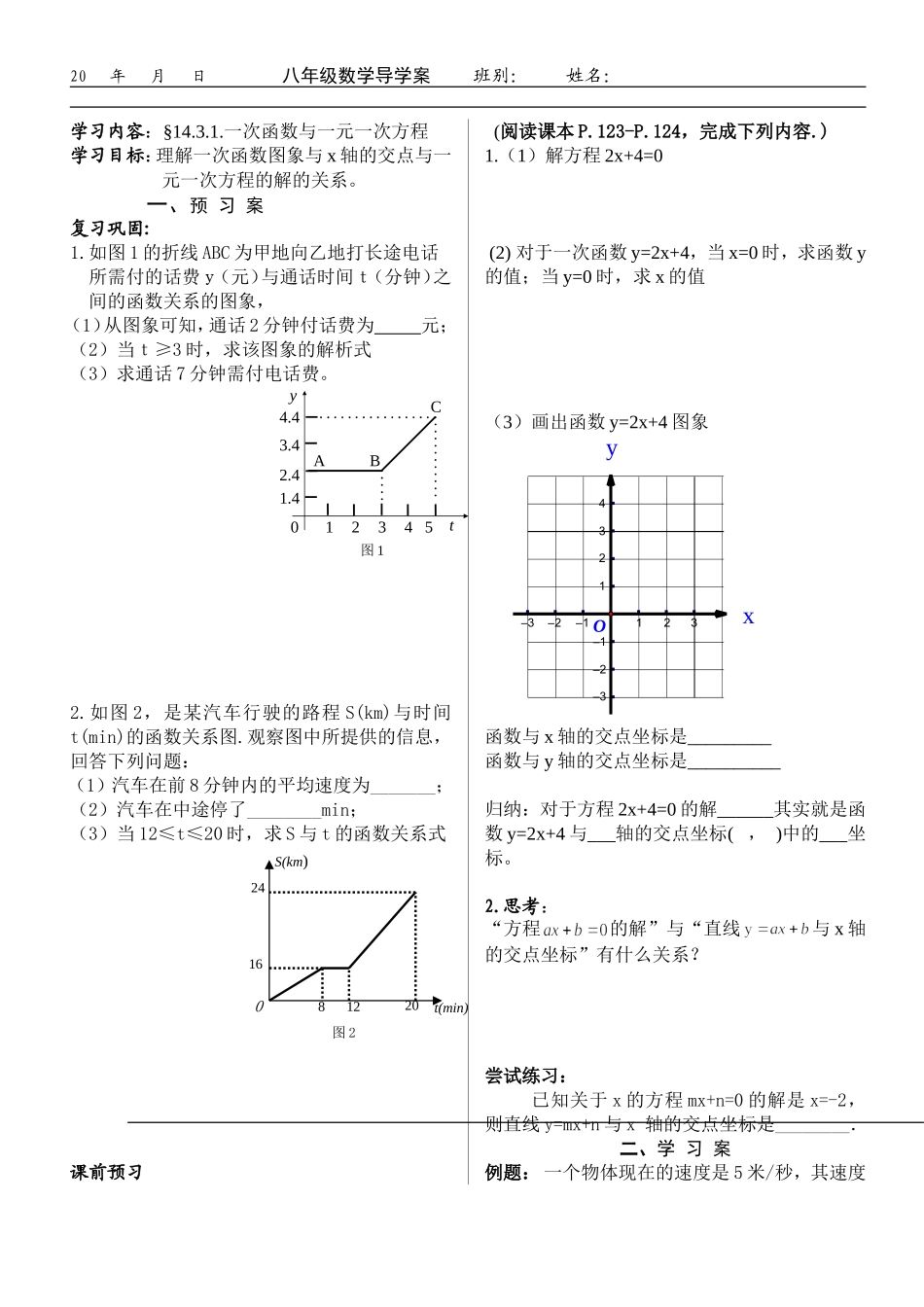
ty012345BAC1.42.43.44.4图1112图224S(km)t(min)16208020年月日八年级数学导学案班别:姓名:学习内容:§14.3.1.一次函数与一元一次方程学习目标:理解一次函数图象与x轴的交点与一元一次方程的解的关系。一、预习案复习巩固:1.如图1的折线ABC为甲地向乙地打长途电话所需付的话费y(元)与通话时间t(分钟)之间的函数关系的图象,(1)从图象可知,通话2分钟付话费为元;(2)当t≥3时,求该图象的解析式(3)求通话7分钟需付电话费。2.如图2,是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,回答下列问题:(1)汽车在前8分钟内的平均速度为_______;(2)汽车在中途停了________min;(3)当12≤t≤20时,求S与t的函数关系式课前预习(阅读课本P.123-P.124,完成下列内容.)1.(1)解方程2x+4=0(2)对于一次函数y=2x+4,当x=0时,求函数y的值;当y=0时,求x的值(3)画出函数y=2x+4图象函数与x轴的交点坐标是_________函数与y轴的交点坐标是__________归纳:对于方程2x+4=0的解______其实就是函数y=2x+4与___轴的交点坐标(,)中的___坐标。2.思考:“方程的解”与“直线与x轴的交点坐标”有什么关系?尝试练习:已知关于x的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是________.二、学习案例题:一个物体现在的速度是5米/秒,其速度yx23–2–3234–2–3–1–111O20年月日八年级数学导学案班别:姓名:每秒增加2米/秒,(1)请写出速度y(m/s)与时间x(s)的函数关系式:。当y=17时,求自变量x的取值。(2).画出速度y与时间x的函数关系式的图象,标出该图象与x轴的交点坐标2、如图所示是某学校以电热水箱的水量y(升)与供水时间x(分)的函数关系(1)求y与x的函数关系式(2)在(1)的条件下,经过多少分钟水箱内有70升水?三、反馈案得分:1、正比例函数经过点(2,1),则正比例函数解析式为:____________________2、(1)方程3x+5=0的解是(2)直线y=3x+5与x轴的交点坐标是3、已知直线y=mx+n与x轴的交点坐标(-5,0),则关于x的方程mx+n=0的解是4、(1)方程2x+1=3x-2的解是(2)直线y=2x+1与y=3x-2的交点坐标是5、已知一次函数y=2x+5与y=5x-1的图像如图,则方程2x+5=5x-1的解为_________。yxy=5x-1y=2x+59026、利用函数图象求方程2x-5=0的解