43空间直角坐标系VIP免费

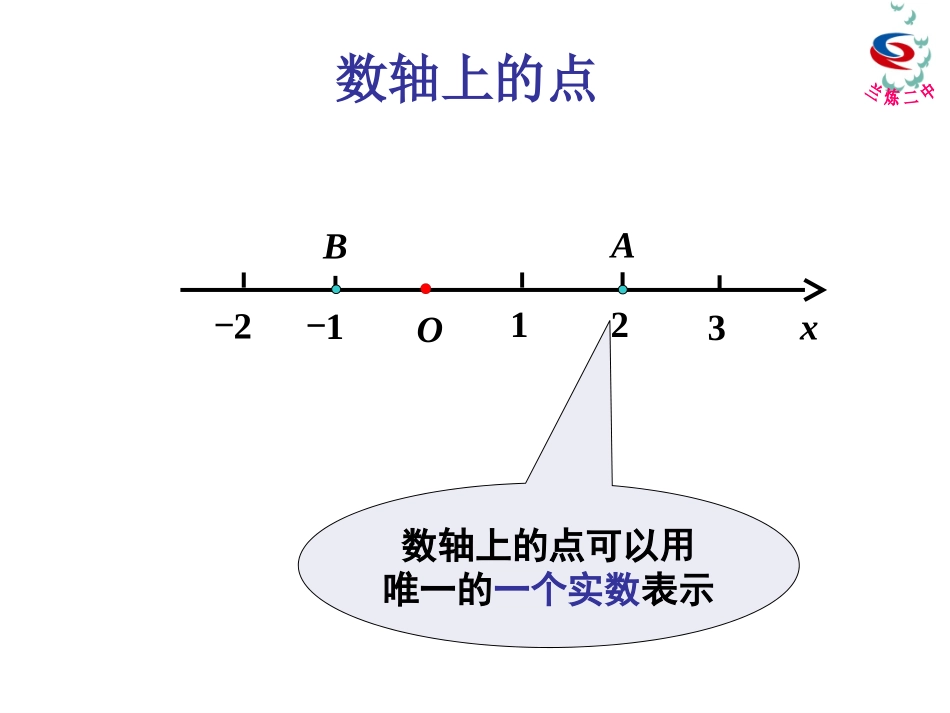
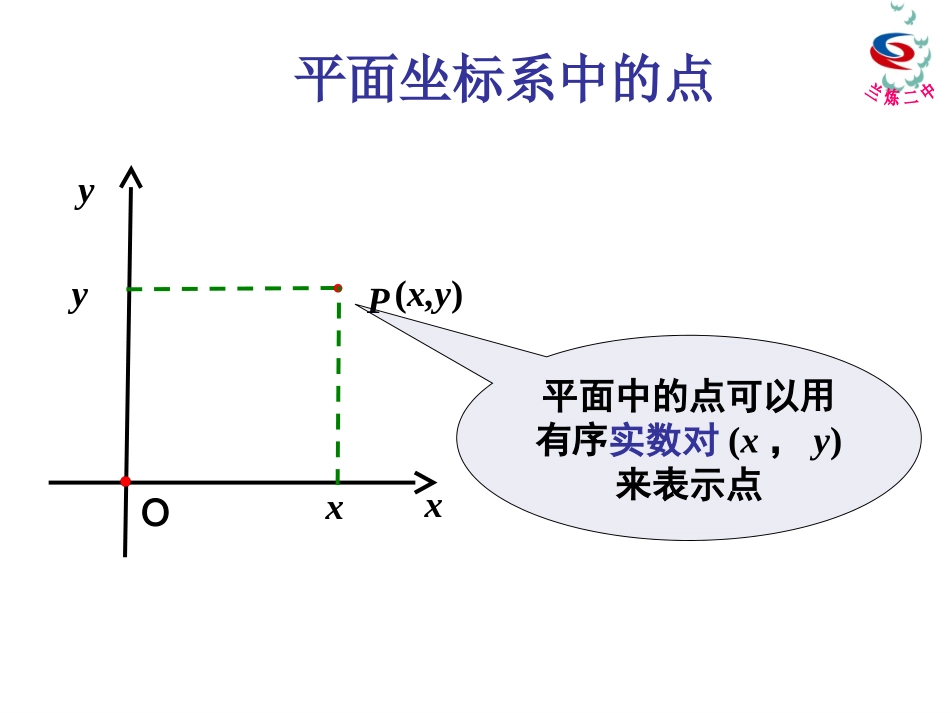
4.3空间直角坐标系xO数轴上的点可以用唯一的一个实数表示-1-2123AB数轴上的点xyPOxy(x,y)平面中的点可以用有序实数对(x，y)来表示点平面坐标系中的点yOx在教室里同学们的位置坐标讲台yOx教室里某位同学的头所在的位置zxo右手直角坐标系空间直角坐标系yz—Oxyz横轴纵轴竖轴111空间的点有序数组),,(zyx11Mxyzo(,,)xyz空间中点的坐标PQRMxyzo(,,)xyz空间中点的坐标（方法二）(0,0,0)PQRA(,0,0)x(0,,0)y(0,0,)z(,,0)xyzoxyB'C'D'CABA'例1.如图,在长方体ABCO-A’B’C’D’中,写点D’,C,A’,B’坐标.2OD'4,OC3,OA解:D’点在z轴上,且OD’=2,所以它的坐标为(0,0,2),C点在y轴上,且OC=4所以它的坐标为(0,4,0)同理点A’坐标为(3,0,2),B’点坐标为(3,4,2)下层:(0,0,0),(1,0,0),(1,1,0),(0,1,0),,021,21zoxy例2.结晶体的基本单位称为晶胞,下图是食盐晶胞的示意图,(可看成是八个长为的小正方体堆积成的正方体),其中白色点代表钠离子,黑色点代表氯离子.如图,建立空间直角坐标系O-xyz后,试写出全部钠离子所在位置坐标21解:把图中钠离子分上中下三层中层:21,210,,21,1,21,21,211,,21,0,21,121,210,1,1,1,1,0,1,0,1,0,0,1,上层:xoyzxoyzxyzo(3,4,3)P136练习2.(0,4,0)3AB'A'D'B'C3C41.52P(1.5,2,3)对称点xyOx0y0(x0,y0)P(x0,-y0)P1横坐标不变，纵坐标相反。(-x0,y0)P2横坐标相反，纵坐标不变。P3横坐标相反，纵坐标相反。-y0-x0(-x0,-y0)空间对称点xoyz1(1,1,1)P(1,1,1)P2(1,1,1)P3(1,1,1)P对称点一般的P(x,y,z)关于：（1）x轴对称的点P1为__________;（2）y轴对称的点P2为__________;（3）z轴对称的点P3为__________;(,,)xyz(,,)xyz(,,)xyz关于谁对称谁不变空间对称点xoyz1(1,1,1)P(1,1,1)P2(1,1,1)P3(1,1,1)Pxyzo空间点到原点的距离ABC(,,)Pxyz||||BPz22||OBxy222||OPxyz两点间距离公式22121212||()()PPxxyy平面：类比猜想22212121212||()()()PPxxyyzz空间：例1求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M三点为顶点的三角形是一个等腰三角形.解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立.例2设P在x轴上，它到)3,2,0(1P的距离为到点)1,1,0(2P的距离的两倍，求点P的坐标.解设P点坐标为),0,0,(x因为P在x轴上，1PP22232x,112x2PP22211x,22x1PP,22PP112x222x,1x所求点为).0,0,1(),0,0,1(•A1(1,4,0)•A(1,4,1)•(2,-2,0)B1•B(2,-2,-1)xOyz111••(-1,-3,0)C1•(-1,-3,3)C2、在空间直角坐标系中作出下列各点(1)、A（1,4,1）；(2)、B（2,-2,-1）；(3)、C（-1,-3,3）；解例3在xoy平面内的直线x+y=1上确定一点M，使M到点N（6，5，1）的距离最小。由已知，可设M（x，1－x，0），则222)10()51()6(xxMN.51)1(22x.51MNmin所以