利用导数研究函数的极值VIP免费

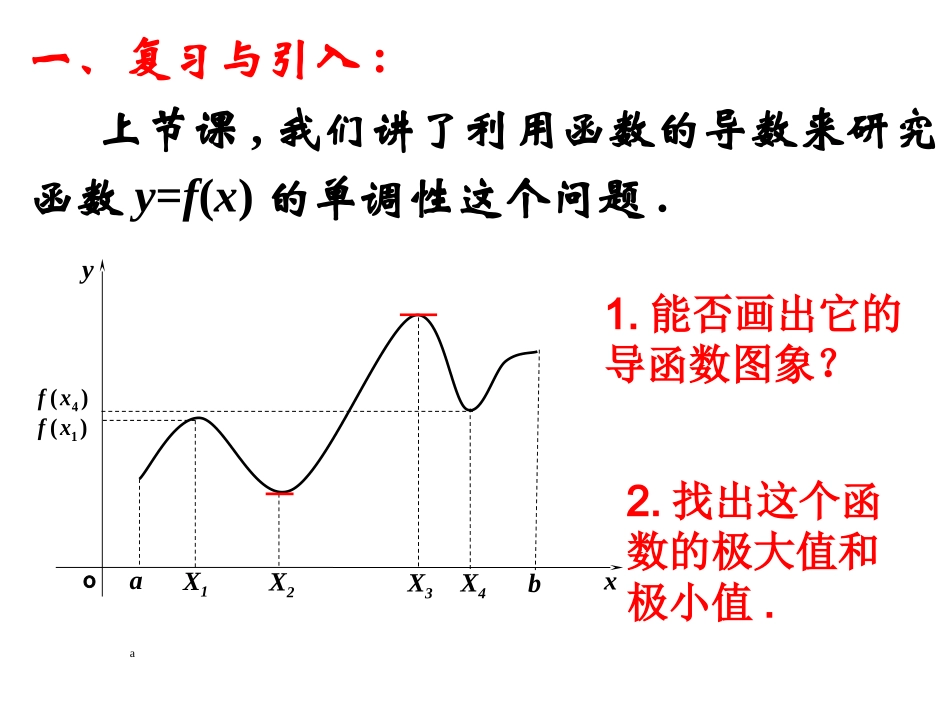
1.3.2导数的应用二利用导数研究函数的极值一、复习与引入:上节课,我们讲了利用函数的导数来研究函数y=f(x)的单调性这个问题.oaX1X2X3X4baxy)(4xf)(1xf1.能否画出它的导函数图象？2.找出这个函数的极大值和极小值.二、新课——函数的极值:一般地,设函数y=f(x)在x0及其附近有定义,如果f(x0)的值比x0附近所有各点的函数值都大,我们说f(x0)是函数y=f(x)的一个极大值;如果f(x0)的值比x0附近所有各点的函数值都小,我们说f(x0)是函数y=f(x)的一个极小值.极大值与极小值统称极值.在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是对应的函数值.(2)函数的极值不是唯一的.即一个函数在某区间上或定义域内极大值或极小值可以不止一个.请注意以下几点:(1)极值是一个局部概念.由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.也就是说极值与最值是两个不同的概念.oaX1X2X3X4baxy)(4xf)(1xf(3)极大值与极小值之间无确定的大小关系.即一个函数的极大值未必大于极小值,如下图所示,x1是极大值点,x4是极小值点,而f(x4)>f(x1).(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点.在上节课中,我们是利用函数的导数来研究函数的单调性的.下面我们利用函数的导数来研究函数的极值问题.由上图可以看出,在函数取得极值处,如果曲线有切线的话,则切线是水平的,从而有f’(x)=0.反过来对吗？如函数y=x3,在x=0处,曲线的切线是水平的,但这点的函数值既不比它附近的点的函数值大,也不比它附近的点的函数值小.假设x0使f’(x)=0.那么在什么情况下x0是f(x)的极值点呢？oaX00bxy0)(0xf0)(xf0)(xf如上图所示,若x0是f(x)的极大值点,则x0两侧附近点的函数值必须小于f(x0).因此,x0的左侧附近f(x)只能是增函数,即f’(x)>0;x0的右侧附近f(x)只能是减函数,即f’(x)<0.oaX0bxy0)(0xf0)(xf0)(xf同理,如上图所示,若x0是f(x)极小值点,则在x0的左侧附近f(x)只能是减函数,即f’(x)<0;在x0的右侧附近只能是增函数,即f’(x)>0.一般地,当函数f(x)在x0处连续时,判别f(x0)是极大(小)值的方法是:(1)如果在x0附近的左侧f’(x)>0,右侧f’(x)<0,那么,f(x0)是极大值;(2)如果在x0附近的左侧f’(x)<0,右侧f’(x)>0,那么,f(x0)是极小值.例1．已知函数y=x3－4x+4，（1）求函数的极值，并画出函数的大致图象；（2）求函数在区间[－3，4]上的最大值和最小值31解：（1）y’=(x3－4x+4)’=x2－4=(x+2)(x－2)31令y’=0，解得x1=－2，x2=2x－2(－2,2)2y’+0－0+y↗极大值↘极小值↗当x变化时，y’，y的变化情况如下表:,22,28343∴当x=－2时，y有极大值且y极大值=328当x=2时，y有极小值且y极小值=－34（2）f(－3)=7，f(4)=9=，31283与极值点的函数值比较得到该函数在区间[－3，4]上最大值是9，最小值是－3134987654321-3-2-143210yx归纳求极值的方法步骤1、求出f’(x)=0的所有x（x1,x2…）;2、列表判断在每个区间上的符号；3、若(a,x1)上f’(x)>0,且(x1，x2)上f’(x)<0,则f(x1)为极大值；若(a,x1)上f’(x)<0,且(x1，x2)上f’(x)>0,则f(x1)为极小值；4、若(a,x1)上f’(x)>0,且(x1，x2)上f’(x)>0,则f(x1)不是极值；求函数y=f(x)在[a，b]的最大（小）值步骤如下：（1）求函数f(x)在开区间(a，b)内所有使f’(x)=0的点；（2）计算函数f(x)在区间内使f’(x)=0的所有点和端点的函数值，其中最大的一个为最大值，最小的一个为最小值。归纳求最值的方法步骤：例2．求y=(x2－1)3+1的极值.解：y’=6x(x2－1)2=6x(x+1)2(x－1)2令y’=0解得x1=－1，x2=0，x3=1.当x变化时，y′，y的变化情况如下表:xx(－∞,－1)－1(－1,0)0(0,1)1(1,+∞)y’－0－0+0+y↘无极值↘极小值0↗无极值↗1-1fx=x2-13+1xOy∴当x=0时，y有极小值且y极小值=0例3．求函数y=x4－2x2+5在区间[－2，2]上的最大值与最小值解：先求导数，得y’=4x3－4x,令y’=0即4x3－4x=0，解得x1=－1，x2=0，x3=1.导数y’的正负以及f(－2)，f(2)如下表：x－2(－2,－1)－1(－1,0)0(0,1)1(1,2)2y’...