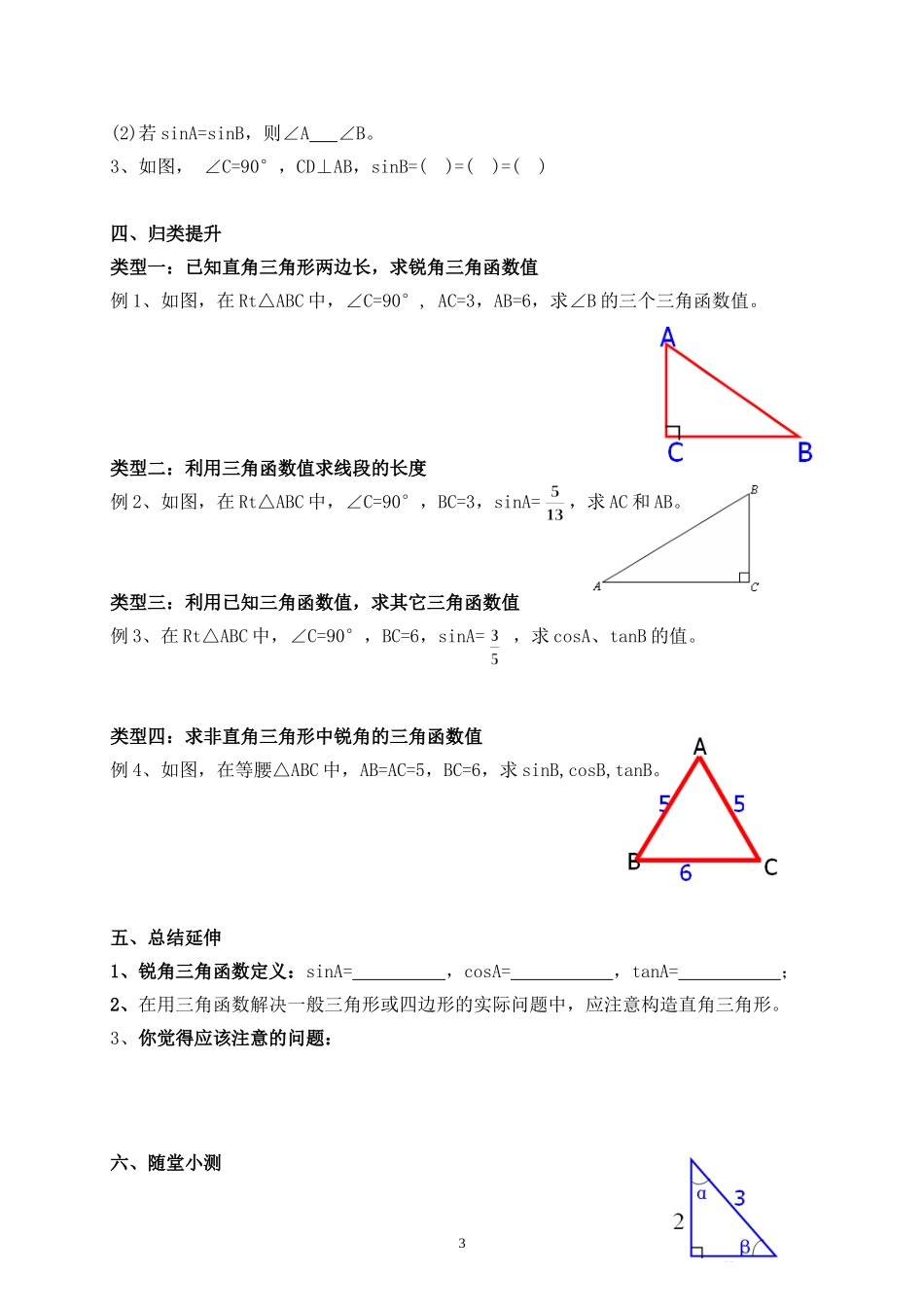
1.1锐角三角函数(第2课时)班级:姓名:一、温故知新1、如图,Rt△ABC中,tanA=,tanB=。2、在Rt△ABC中,∠C=90°,tanA=,AC=10,求BC,AB的长。3、若梯子与水平面相交的锐角(倾斜角)为∠A,∠A越大,梯子越;tanA的值越大,梯子越。4、当Rt△ABC中的一个锐角A确定时,其它边之间的比值也确定吗?可以用其它的方式来表示梯子的倾斜程度吗?二、探究新知探究1:如图,请思考:(1)Rt△AB1C1和Rt△AB2C2的关系是;(2);(3)如果改变B2在斜边上的位置,则;思考:从上面的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________,根据是______________________________________。它的邻边与斜边的比值呢?归纳概念:1、正弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边BC与斜边AB的比叫做∠A的正弦,记作sinA,即:sinA=________。2、余弦的定义:1B1B2AC1C2ACB如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边AC与斜边AB的比叫做∠A的余弦,记作cosA,即:cosA=______。3、锐角A的正弦,余弦,正切和余切都叫做∠A的三角函数。温馨提示:(1)sinA,cosA是在直角三角形中定义的,∠A是一个锐角;(2)sinA,cosA中常省去角的符号“∠”。但∠BAC的正弦和余弦表示为:sin∠BAC,cos∠BAC。∠1的正弦和余弦表示为:sin∠1,cos∠1;(3)sinA,cosA没有单位,它表示一个比值;(4)sinA,cosA是一个完整的符号,不表示“sin”,“cos”乘以“A”;(5)sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长没有必然的关系。探究2:我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?探索发现:梯子的倾斜程度与sinA,cosA的关系:sinA越大,梯子;cosA越,梯子越陡。探究活动3:如图,在Rt△ABC中,∠C=90°,AB=20,sinA=0.6,求BC和cosB。通过上面的计算,你发现sinA与cosB有什么关系呢?sinB与cosA呢?在其它直角三角形中是不是也一样呢?请举例说明。小结规律:在直角三角形中,一个锐角的正弦等于另一个锐角的。三、及时检测1、如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值()A、扩大100倍B、缩小100倍C、不变D、不能确定2、已知∠A,∠B为锐角(1)若∠A=∠B,则sinAsinB;2ABC(2)若sinA=sinB,则∠A∠B。3、如图,∠C=90°,CD⊥AB,sinB=()=()=()四、归类提升类型一:已知直角三角形两边长,求锐角三角函数值例1、如图,在Rt△ABC中,∠C=90°,AC=3,AB=6,求∠B的三个三角函数值。类型二:利用三角函数值求线段的长度例2、如图,在Rt△ABC中,∠C=90°,BC=3,sinA=,求AC和AB。类型三:利用已知三角函数值,求其它三角函数值例3、在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值。类型四:求非直角三角形中锐角的三角函数值例4、如图,在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB。五、总结延伸1、锐角三角函数定义:sinA=,cosA=,tanA=;2、在用三角函数解决一般三角形或四边形的实际问题中,应注意构造直角三角形。3、你觉得应该注意的问题:六、随堂小测3CEADFB1、如图,分别求∠α,∠β的三个三角函数值。2、在等腰△ABC中,AB=AC=13,BC=10,求sinB,cosB。3、在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4。求:CD和sinC。4、在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5。求sin∠ACD,cos∠ACD和tan∠ACD。5、在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18,求sinB,cosB,tanB。6、如图,在△ABC中,点D是AB的中点,DC⊥AC,且tan∠BCD=1/3。求∠A的三个三角函数值。4