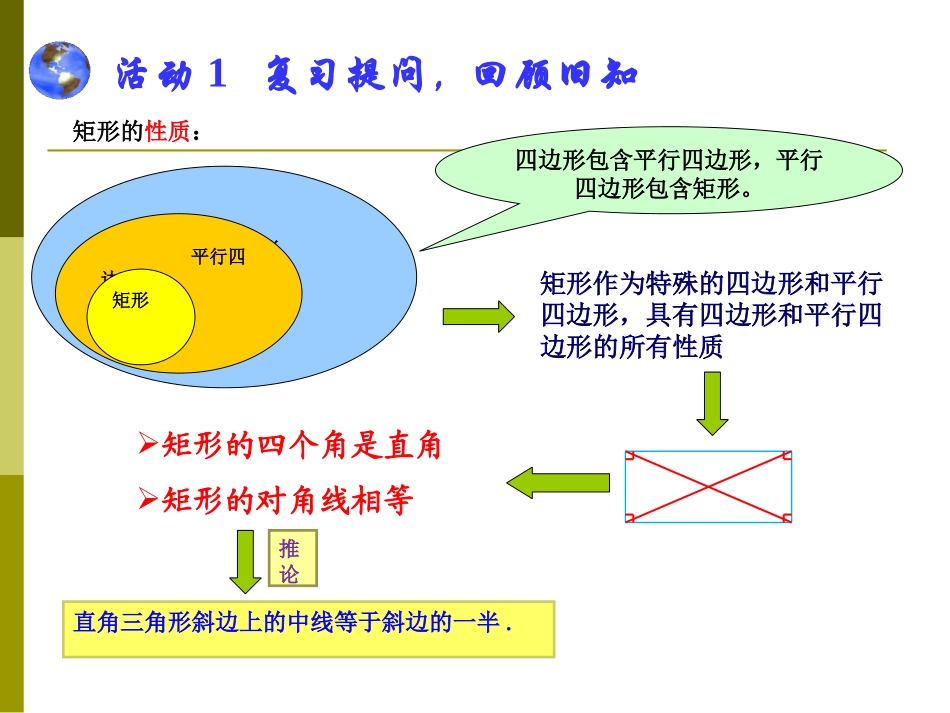
活动1复习提问,回顾旧知根据平行四边形、矩形的定义填空:四边形平行四边形矩形()()两组对边分别平行有一个角是直角矩形的性质:四边形平行四边形矩形矩形作为特殊的四边形和平行四边形,具有四边形和平行四边形的所有性质矩形的四个角是直角矩形的对角线相等直角三角形斜边上的中线等于斜边的一半.推论四边形包含平行四边形,平行四边形包含矩形。活动1复习提问,回顾旧知活动2小题训练、夯实基础根据矩形的性质填空:1.如图:点A是圆弧上一动点,点C是x轴正半轴上一动点,BC∥OA,AB∥x轴,①四边形OABC是?yxOABC②当A运动到y轴时,四边形OABC是?2.如图:矩形ABCD中,∠ABO=30°,则∠ACB为()AA.60°B.70°C.80°D.90°平行四边形矩形请找出关键词,画上横线、标图,并思考本题考察了什么知识点?考察的知识点:平行四边形和矩形的定义考察的知识点:矩形的四个角都是直角。根据矩形的性质填空:53.矩形ABCD中,边AB=2,BC=求:BD的长为______.ODCBA4.若直角三角形的两条直角边长分别为6和8,则斜边上的中线长是()A.3B.4C.5D.1023C3232活动2小题训练、夯实基础请找出关键词,画上横线、标图,并思考本题考察了什么知识点?考察的知识点:直角三角形斜边上的中线等于斜边的一半。考察的知识点:勾股定理和矩形的对角线相等且四个角为直角。活动3大题训练、感悟方法1、矩形对角线相等的性质应用如图在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,求证:△ACE是等腰三角形。证明等腰三角形边相等平行四边形性质矩形对角线相等全等三角形……EABCD等角对等边回忆一下证明等腰三角形的方法有哪些?方法1:利用矩形对角线相等和平行四边形性质等有关知识进行等量代换矩形ABCDABCD∥AC=BDDBCE∥四边形BECD是平行四边形BD=CEAC=EC得证EABCD如图在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,求证:△ACE是等腰三角形。分析:DBCE∥纵向思维:方法2:利用等角对等边证明矩形ABCDOA=OBDBCE∥∠OAB=OBA∠∠OAB=E∠得证∠OBA=E∠AC=EC方法3:请同学课下自己完成EABCDo活动3大题训练、感悟方法如图在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,求证:△ACE是等腰三角形。2.矩形四个角都是直角的性质应用在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,EF=AE你能证明FE⊥AE吗?横向思维:证明垂直的方法一个角为直角或两个锐角之和为90°1FEDABC23等腰三角形三线合一矩形的四个角为90°勾股定理逆定理……活动3大题训练、感悟方法纵向思维:矩形ABCD∠D=C=ABC=90°∠∠BE平分∠ABC∠D=C=90°∠CE=CB∠1=2∠∠CEB=CBE=45∠AD=CE1FEDABC23AD=BCEF=AE△ADEECF△∠2+3=90°∠∠1+3=90°∠FEAE⊥活动3大题训练、感悟方法在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,EF=AE,你能证明FE⊥AE吗?3.直角三角形斜边中线等于斜边一半的性质应用如图,BD、CE是△ABC的高,G、F分别是BC、DE的中点,求证:FG⊥DE.横向思维:证明垂直的方法一个角为直角或两个锐角之和为90°等腰三角形三线合一矩形的四个角为90°勾股定理逆定理……AEBGCDF活动3大题训练、感悟方法纵向思维:BD⊥ACCE⊥ABG是BC中点F是ED中点连接DG、EGDG=1/2BCEG=1/2BCDG=EG三线合一FG⊥DEAEBGCDF活动3大题训练、感悟方法如图,BD、CE是△ABC的高,G、F分别是BC、DE的中点,求证:FG⊥DE.问题横向思维结论纵向思维方法1方法2方法3……活动3方法归纳活动4课堂小结本节课复习了哪些知识?在审题时应该怎么样做?在解决几何问题时应该如何思考?活动5课堂检测布置作业如图在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,如果FEAE⊥,求证FE=AE。FEDABC作业:全品作业手册矩形性质及应用由于本人对知识理解还很浅薄,谢谢大家为我多多提出宝贵的修改意见。