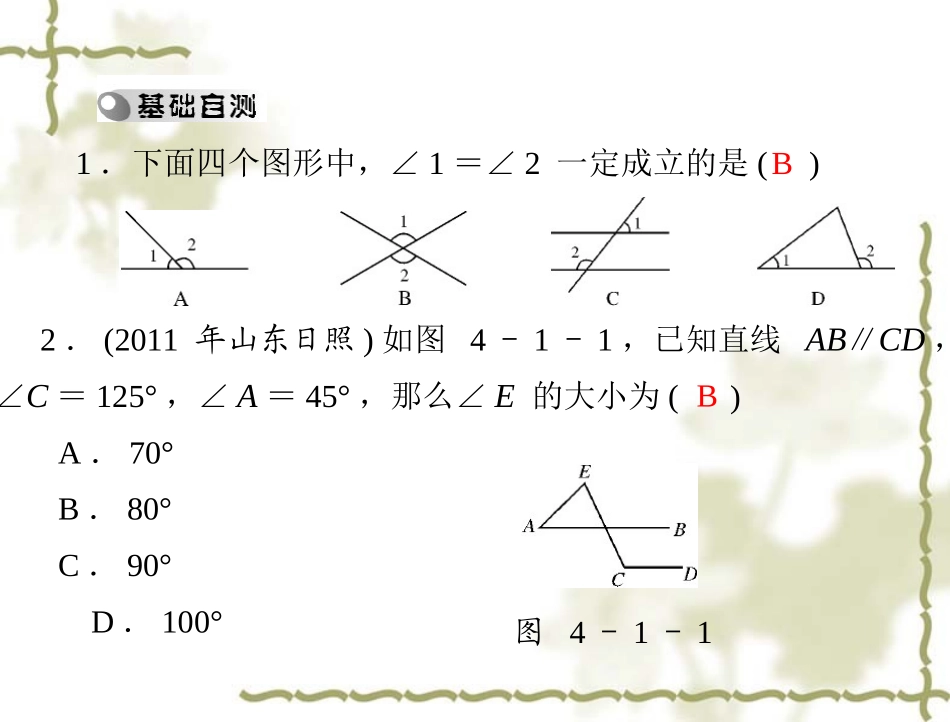
题设结论真命题假命题定理证明5.命题、定理、证明(1)命题:判断一件事情的语句叫做命题,每个命题都是由________和________两部分组成.(2)真命题和假命题:正确的命题叫做__________;错误的命题叫做__________.(3)用推理的方法判断为正确的命题叫做________.(4)从一个命题的题设出发,通过推理来判断命题是否成立的过程叫做________.BB1.下面四个图形中,∠1=∠2一定成立的是()2.(2011年山东日照)如图4-1-1,已知直线AB∥CD,)∠C=125°,∠A=45°,那么∠E的大小为(A.70°B.80°C.90°D.100°图4-1-13.(2012年北京)如图4-1-2,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM=()A.38°D.144°B.104°图4-1-2C.142°图4-1-34.将一直角三角板与两边平行的纸条按如图4-1-3所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的个数是()CDA.1个B.2个C.3个D.4个5.有如下命题:①三角形的内角和等于180°;②两直线平行,同位角相等;③矩形的对角线相等;④相等的角是对顶角.其中属于假命题的有__________(填序号).④考点1余角、补角、对顶角154A.35°B.55°C.65°D.145°1.(2011年广东广州)已知∠α=26°,则∠α的补角是________度.2.(2011年广东清远)已知∠α=35°,则∠α的余角是()B3.(2011年广东湛江)如图4-1-4,直线AB,CD相交于)B点E,DF∥AB,若∠AEC=100°,则∠D=(图4-1-4A.70°B.80°C.90°D.100°规律方法:互为余角的两个角的和为90°,互为补角的两个角的和为180°,对顶角相等.考点2平行线的性质与判定4.(2011年广东茂名)如图4-1-5,已知AB∥CD,则图中与∠1互补的角有()ACA.2个B.3个C.4个D.5个图4-1-5图4-1-65.(2010年广东)如图4-1-6,已知∠1=70°,如果CD∥BE,那么∠B的度数为()A.70°B.100°C.110°D.120°6.(2009年广东清远)如图4-1-7,AB∥CD,EF⊥AB于)点E,EF交CD于点F,已知∠1=60°,则∠2=(图4-1-7A.20°B.60°C.30°D.45°规律方法:在平行线与相交线的角度计算中,主要运用:①两直线平行,同位角相等,内错角相等,同旁内角互补;②对顶角相等;③余角、补角性质.C考点3角平分线、线段的垂直平分线的应用例题:(2009年广东肇庆节选)如图4-1-8,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE.求证:∠CBE=36°.图4-1-8 AB=AC,∠A=36°,∴∠ABC=∠C=72°.∴∠CBE=∠ABC-∠EBA=36°.证明: DE是AB的垂直平分线,∴EA=EB.∴∠EBA=∠A=36°.7.(2011年广东茂名)如图4-1-9,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5千米,村庄C到公路l1的距离)B为4千米,则村庄C到公路l2的距离是(图4-1-9A.3千米B.4千米C.5千米D.6千米.已知:如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是()A.60°B.80°C.100°D.120°如图,地面上有一个钟,钟面12个粗线段刻度是整点时时针(短针)所指位置.由图中时针与分针(长针)所指位置,该钟面所显示的时刻是______时_______分.图6学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)):从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A.①②B.②③C.③④D.①④20PD=PC图4-1-10图4-1-119.(2008年广东肇庆)如图4-1-11,P是∠AOB的角平分线上的一点,PC⊥OA于点C,PD⊥OB于点D,写出图中一对相等的线段_____________(答案不唯一,只需写出一对即可).8.(2011年广东汕头模拟)如图4-1-10,在△ABC中,DE垂直平分AC交AB于点E,若△BCE的周长为12cm,AC=8cm,则△ABC的周长为________cm.考点4命题与证明10.(2012年广东深圳)下列命题:D①方程x2=x的解是x...