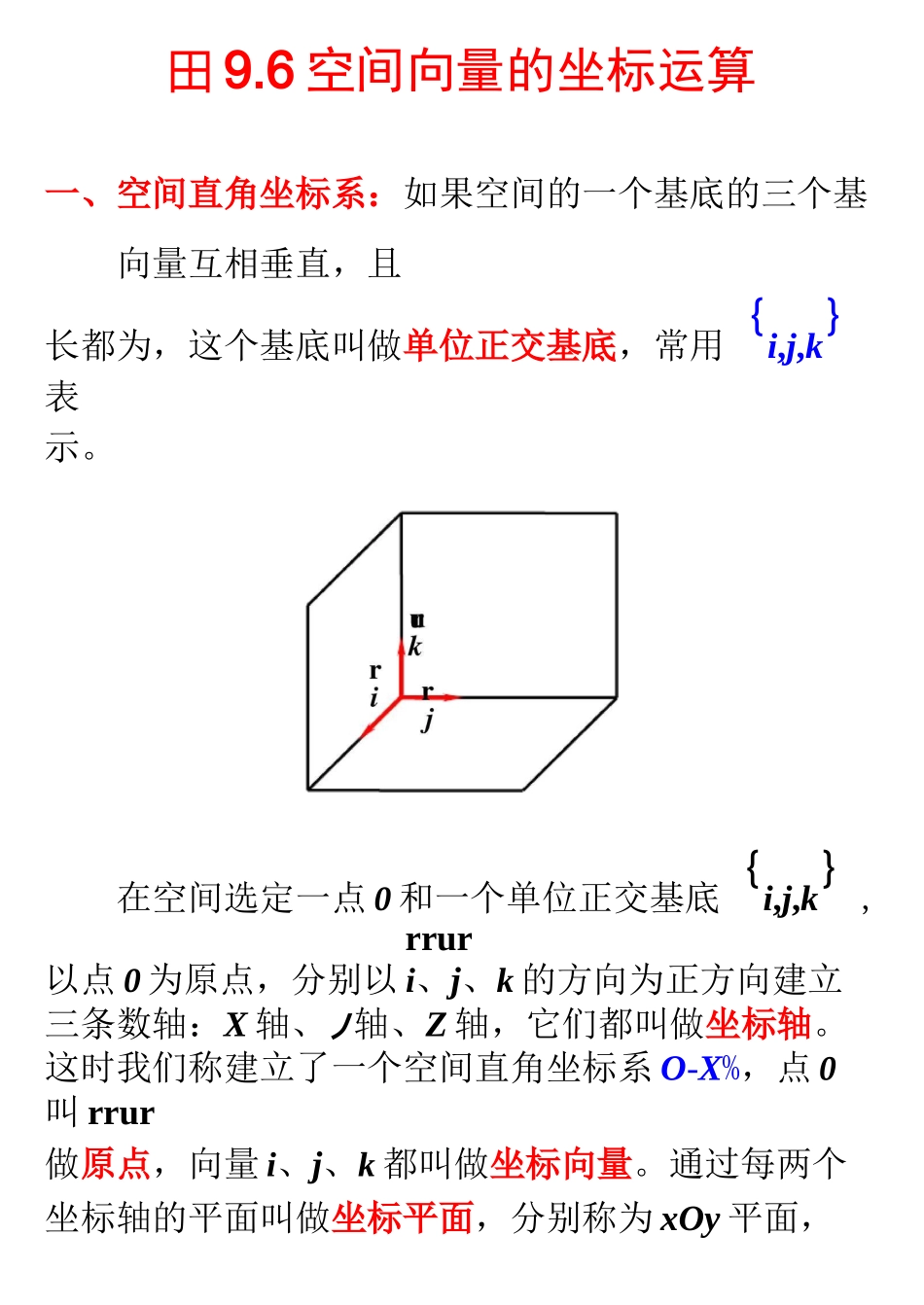
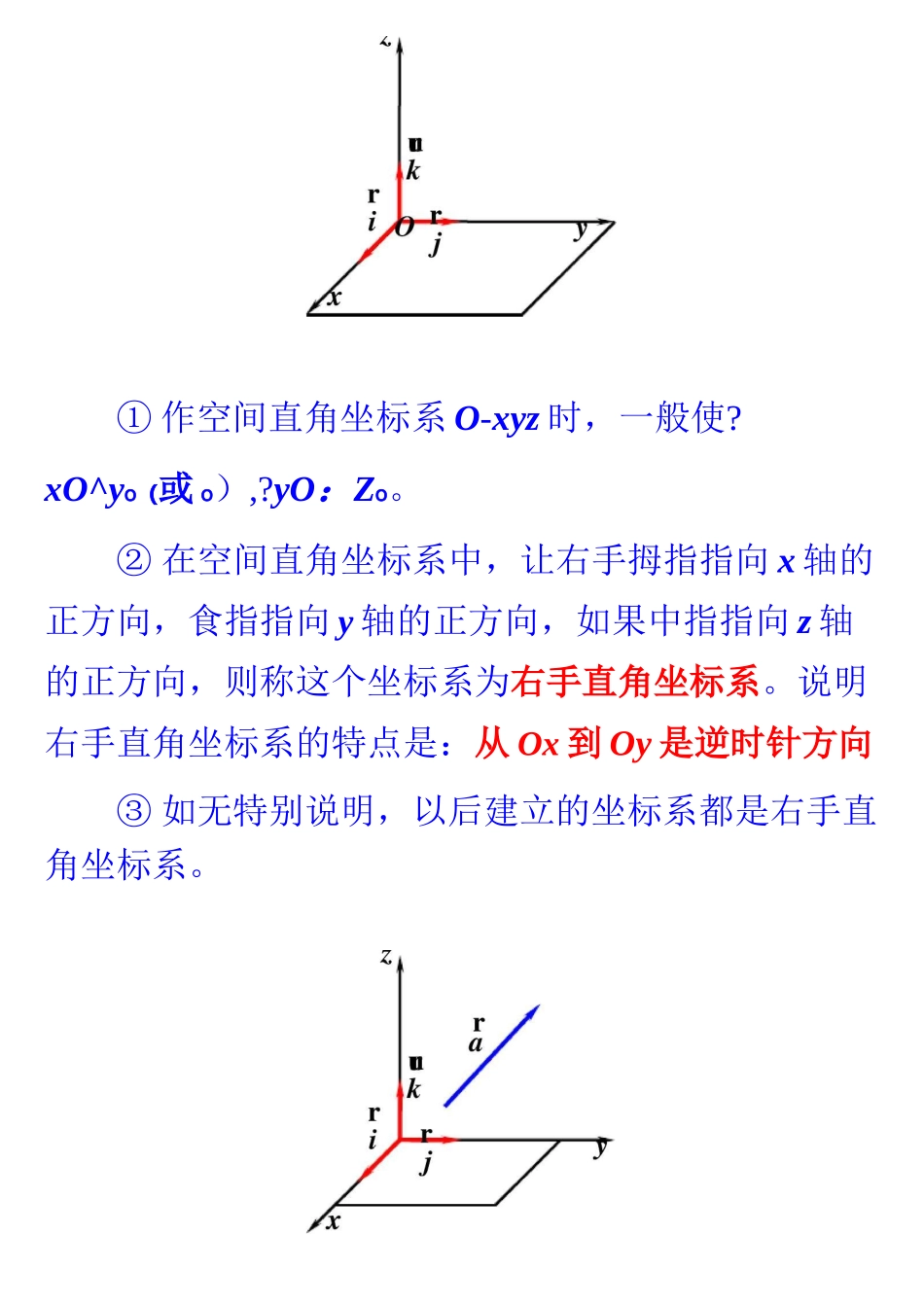
田9.6空间向量的坐标运算一、空间直角坐标系:如果空间的一个基底的三个基向量互相垂直,且长都为,这个基底叫做单位正交基底,常用{i,j,k}表示。在空间选定一点0和一个单位正交基底{i,j,k},rrur以点0为原点,分别以i、j、k的方向为正方向建立三条数轴:X轴、丿轴、Z轴,它们都叫做坐标轴。这时我们称建立了一个空间直角坐标系O-X%,点0叫rrur做原点,向量i、j、k都叫做坐标向量。通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面,yOz平面,zOx平面。①作空间直角坐标系O-xyz时,一般使?xO^yo(或o),?yO:Zo。②在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系。说明右手直角坐标系的特点是:从Ox到Oy是逆时针方向③如无特别说明,以后建立的坐标系都是右手直角坐标系。rrr给定一个空间直角坐标系和向量a,且设i、八urk为坐标向量,根据空间向量基本定理可知:存在唯一的有序实数组(a,a,a),使rrrua=ai+aj+akr有序实数组(a,a,a)叫做向量a在空间直角坐标系O-卩z中的坐标,可简记作ra=(a,a,a)在空间直角坐标系O-兀%中,对空间任一点A,uuur对应一个向量OA,于是存在唯一的有序实数组x、八z,使uuurrrurOA=xi+yj+zk有序实数组(x,y,z)叫做点A的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的①AB的中点坐标(x+xy+y纵坐标,z叫做点A的竖坐标二、空间向量的直角坐标运算:rrI・设a=(a,a,a),b=(b,b,b),则rr①a+b=(a+b,a+b,a+b);rr②a-b=(a-b,a-b,a-b);r③la=(la,la,la)(I?R);rr④a?ab+ab+ab;rr⑤a八b?abab+ab=;::a=lbrr⑥a//b?1alb(I?R)。Ia=lbII・若A(兀,J,z)、B(x,y,z),则uuuruuuruuur②AB=OB-OA=(x-x,y-y,z-z)。说明:一个向量在直角坐标系中的坐标等于表示z+zrrr,,),b=(,m,-),且a?,B)D)uur4、已知°为直角坐标原尿这个向量的有向线段的终点的坐标减去起点的坐标。r1、若a=(-则m=(A)(C)2、点P(,-,)关于原点对称的点P如勺坐标是3、设点M(,-,),N是点P(,,)在坐标平uuuur面xOy内的射影,则MN的坐标是。OB=(-,,),OC八OA,BC//OA,求AC。rr5、右。=(r?,-r),r=(-,,)。①若〈ka+b)//(a-b),求实数k的值;uu9②若QQ+b)A(a-b),求实数氐的值。6、如图,在正方体ABCD-ABCD中,E、F分别是BB、BD的中点,求证:EFAAD。7、如图,在正方体ABCD-ABCD中,E、F分别是BB、CD的中点,求证:DFA平面ADE。DCMr\aVb三、夹角和距离公式:rrI・右a=(a,a,a),b=(b,b,b),则rrr①Ia=Ja?rrrIb=Jbbrr②cosa?II・若A(兀,j,z),B(x,y,z),贝UuunIAB\=J;(x-x)+(y-y)+(z-z)或dAB=x-x)+(y-y)+(z-z)其中dAR表示A与B两点间的距离,这就是空间AB两点间的距离公式。+a+a+b+brab+ab+ab1、在正方体ABCD-ABCD中,E、F分别是AA、CC的中点,则直线DE与DF所成角的余弦值是(A)_(B)_(C)_(D)£2、在棱长为的正方体ABCD-ABCD中,O是底面ABCD的中心,E、F分别是CC、AD的中点,那么异面直线OE和DF所成的角的余弦值等于(A)厂(B)_(C)厂(D)厂3、如图,直棱柱ABC-ABC的底面DABC中,CA=CB=,?ACBo,棱AA=,M、N分别是AB、AA的中点。umr①求IBNI;②求证:AB八CM;③求AB与BC的夹角。5、如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG八平面ABCD,垂足为G,G在AD上,且PG=,AG=GD,BG八GC,GB=GC=,E是BC的中点。①求异面直线GE与PC所成的角的余弦值;②若F点是棱PC上一点,且DF八GC,求PF的FC值。P四、平面的法向量:丨■平面法向量定义:r①如果表示向量a的有向线段所在直线垂直于平r面a,则称这个向量垂直于平面a,记作a人ax二向量,则可取n=桫zxz、T・;-T1-:ra?rrnrr即可得到rr②如果a人a,那么向量a叫做平面a的法向量II■平面的方程:①舟殳式:Ax+By+Cz+D=;②截距式:x+y+z=。abcIII.如何求平面的法向量:方法一:利用平面方程求法向量。若平面a的方程是Ax+By+Cz+D=,则a的r一个法向量是n=(A,B,C)。方举三:利用平面内不共线二向量求法向量。设a、b是平面a内不共线二向量,a的法向量是rrrrn=(x,y,z(或n=(,y,z)或n=(x,,z)或n=(x,y,)方法三:利用向量的外积求法向量。rr若a=(x,y,z)、b=(x,y,z)是a内不共线(其中二阶行列式ad=ad-be)在如图所示的空间直角坐标系中,E是正方体ABCD-ABCD的棱BB的中点,F在CD上,且