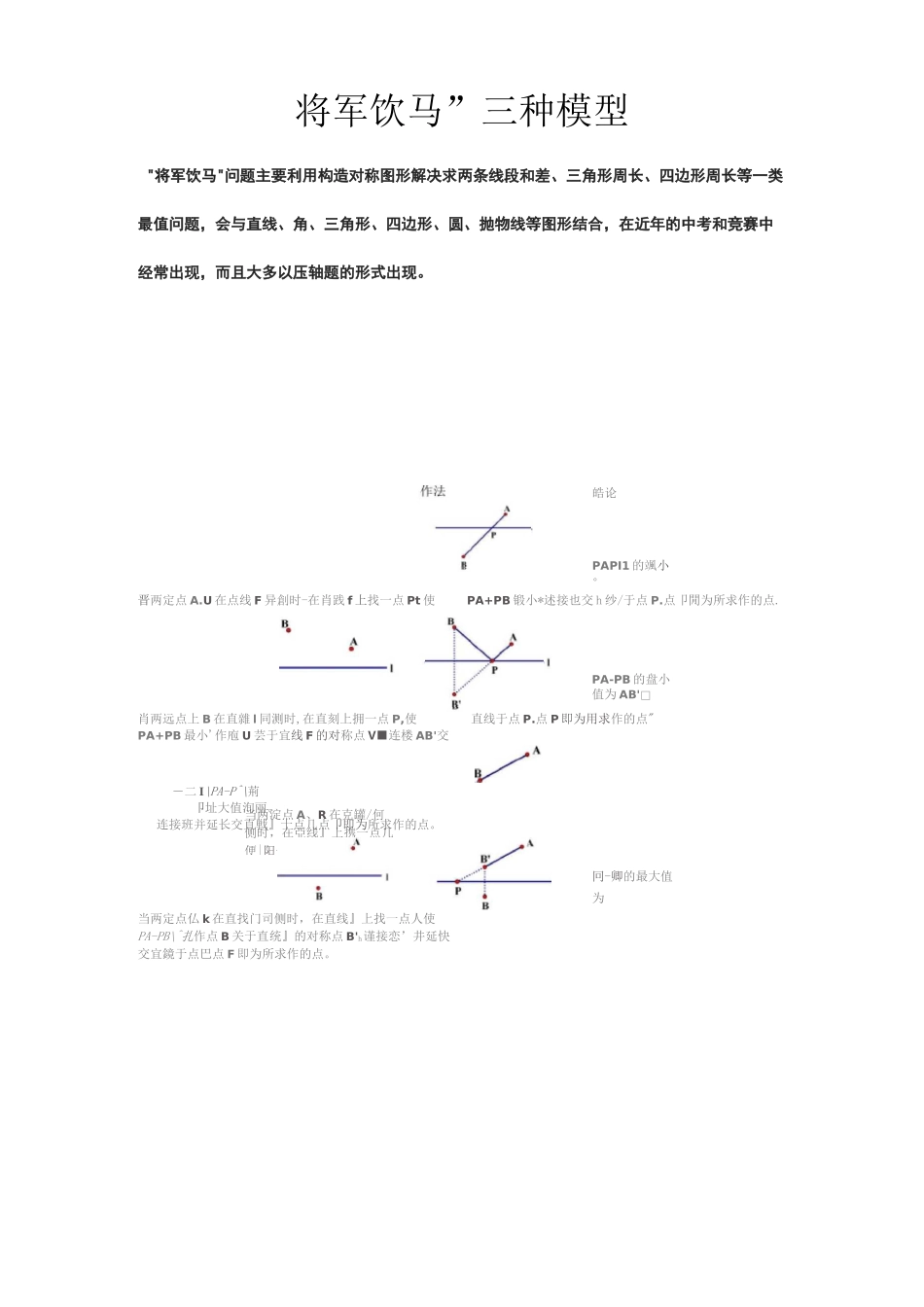
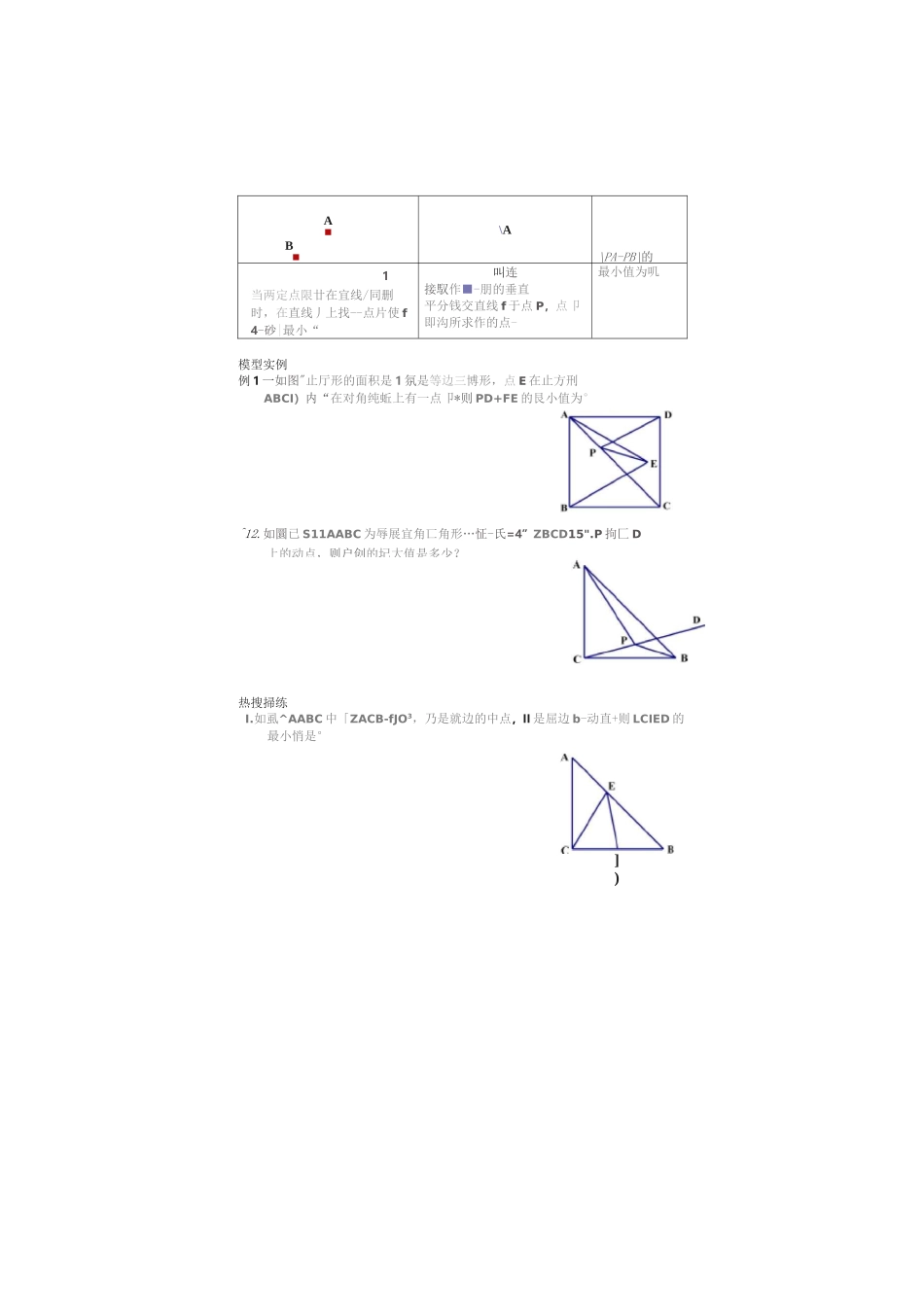
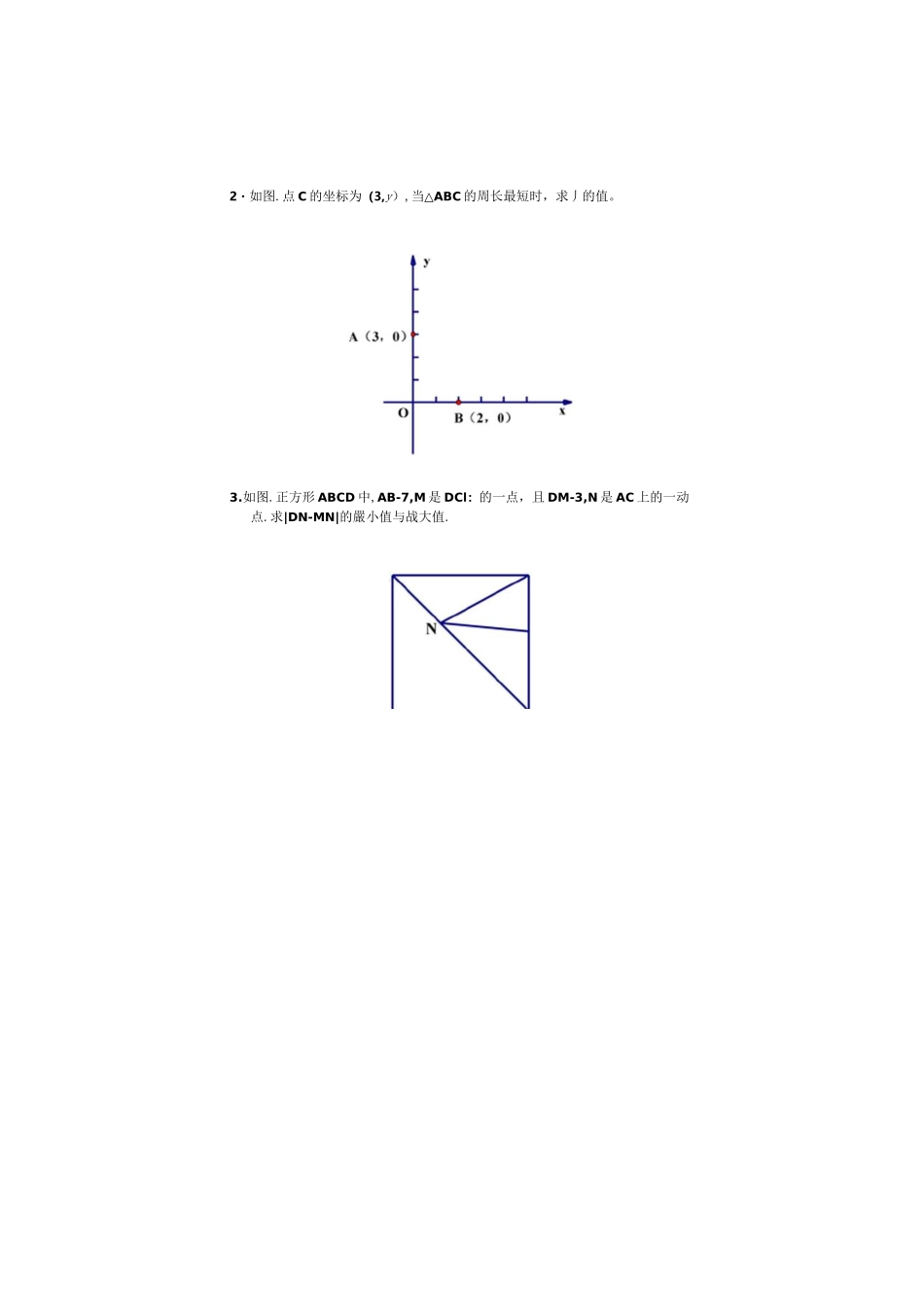
当两淀点A、R在克罐/何侧时,在亞线』上携一点几便|阳一户创最大°将军饮马”三种模型"将军饮马"问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现。晋两定点A.U在点线F异創时-在肖践f上找一点Pt使PA+PB锻小*述接也交h纱/于点P.点卩閒为所求作的点.肖两远点上B在直雜I同测时,在直刻上拥一点P,使PA+PB最小'作庖U芸于宜线F的对称点V■连楼AB'交直线于点P.点P即为用求作的点"―二I\PA-P^\荊卩址大值洵丽。连接班并延长交直戦』十点几点卩即为所求作的点。当两定点仏k在直找门司侧时,在直线』上找一点人使PA-PB\^扎作点B关于直统』的对称点B'h谨接恋’井延快交宜鏡于点巴点F即为所求作的点。皓论PAPI1的颯小°PA-PB的盘小值为AB'□冋-卿的最大值为上的动点,则户创的圮大值是多少?A■B■\A\PA-PB\的1当两定点限廿在宜线/同删时,在直线丿上找--点片使f4-砂|最小“叫连接馭作■-朋的垂直平分钱交直线f于点P,点卩即沟所求作的点-最小值为叽模型实例例1一如图"止厅形的面积是1氛是等边三博形,点E在止方刑ABCI)内“在对角纯蚯上有一点卩*则PD+FE的艮小值为°^12.如圜已S11AABC为辱展宜角匸角形…怔-氏=4”ZBCD15".P拘匚D热搜掃练I.如虱^AABC中「ZACB-fJO3,乃是就边的中点,II是屈边b-动直+则LCIED的最小悄是°])2・如图.点C的坐标为(3,y),当△ABC的周长最短时,求丿的值。3.如图.正方形ABCD中,AB-7,M是DCI:的一点,且DM-3,N是AC上的一动点.求|DN-MN|的嚴小值与战大值.△PCD周氏最点P在ZAOB的内部,在0B上找点D,在0A上找点C,使得△PCD周长最小。分别作点P关于OA、0B的对称点P‘.PS连接P,PS交()A、0B于点C、D,点C、I)即为所求。点P在ZAOB的内部,在0B上找点D,在0A上找点C,使得PDWDG小。作点P关干0B的对称点P',过点P'作P‘C丄0A交0B干点C,点C、D幼为所求,点氏Q在ZA0B的内部.在0B上找点D.在0A上找点C,使得四边形PQDC周长瑕小。分别作点人Q关于0A.0B的对称点A、Q*,连接P‘,交OA、0B于点C、D,点C.D即为所求。POCD+DQ的最小值为I"Q',所以四边形PQDC的周长的最小值为P;Q'4PQO模型2角到定点作法结论PCKD的最小值为P'CoI)模型实例例1・如图.ZAOB=30°,ZAOB内有一定点P,且OP=10,在0A上有一点Q・0B上冇一点R。若周长最小,则鼓小周长是多少?热搜将练L如图,ZMON二40°,卩为上如"内一定点,A为CM上的点,B为0N上的点,当APAB的周长取最小值时:(1)找到A.8点・保留作图痕迹;(2)求此时ZAPB等于多少度。如果ZMO20,ZAPB又等于多少度?2.如图,四边形ABCD中,ZBAD=110°,ZB=ZD=90°,在BC、CD上分别找一点爪N,使ZSAMN周长最小,并求此时ZAMN+ZANM的度数。3・如图.在x轴匕找一点C,在丿轴上找」点D.使ADWD+BC最小.并求直线CD的解析式及点C、【)的坐标。MNy■-••A(I,3>-•11(3,1>1丄1丄'丄()"4.如图ZMO\=20°,A、B分别为射线OM、ON上两定点,IL0A=2,0B=4.点P、Q分别为射线凶、ON上两动点,当人Q运动时,线段AQHP+PB的最小值是多少?模型3两定点一定长模型作法结论dA*一*B■1£亠\/ZAM+NN+NB最小为YBo如图,在宜线/上找M、N两点(M在左〉,使得/VM+MN+NBft小,且MN=〃°SMA!/\/•将点A向右平移“个单位到A'•作A'关于直线/的对称点AS连按YB交直线/丁•点N,将点N向左平移d个单位到\1,点M、N即为所求。A•jAM+MN^XB的嚴小值为”B+d。«i7ETZh•B如图,/|〃厶,小厶Z间距离为d,在厶,厶分别找M、N两点,使得MN丄,11AM+MN+NB最小。B将点A向下平移〃个单位fiJ.V,连接MB交宜线A于点N,将点X向上平移d个单位到曲点M、NBP为所求。模型实例例i・在平面直角坐标系中.矩形OABCm所示,点A在K轴正半轴上,点C&y轴正半轴上,且0A=6,0C=4,D为0C中点,点E、F在线段0A上,点E在点F左侧,EF=2°当四边形BDEF的周长最小时,求点E的坐标。】,在卩酣旬用坐标系屮,佢形锻CU的顶点0在坐标廈点.顶点LB分刖在,x轴,了轴的正半轴IhA(3,0)、R(山4〉•D为边朋的屮点"(I)若EM0A匕吋一个动点"求DCJE的周长最小恒:傭)若E、F为边CA上的两个动点.且EF=L"U'g边形CDEF的周长最小时*求点匚F的坐标。2.村.TAfll村庄Rii于一条小何的两侧,若河岸彼此平fF,要架设一座□河岸垂覆的桥.桥址应如诃选择.才便A与卩/间的距离最短?