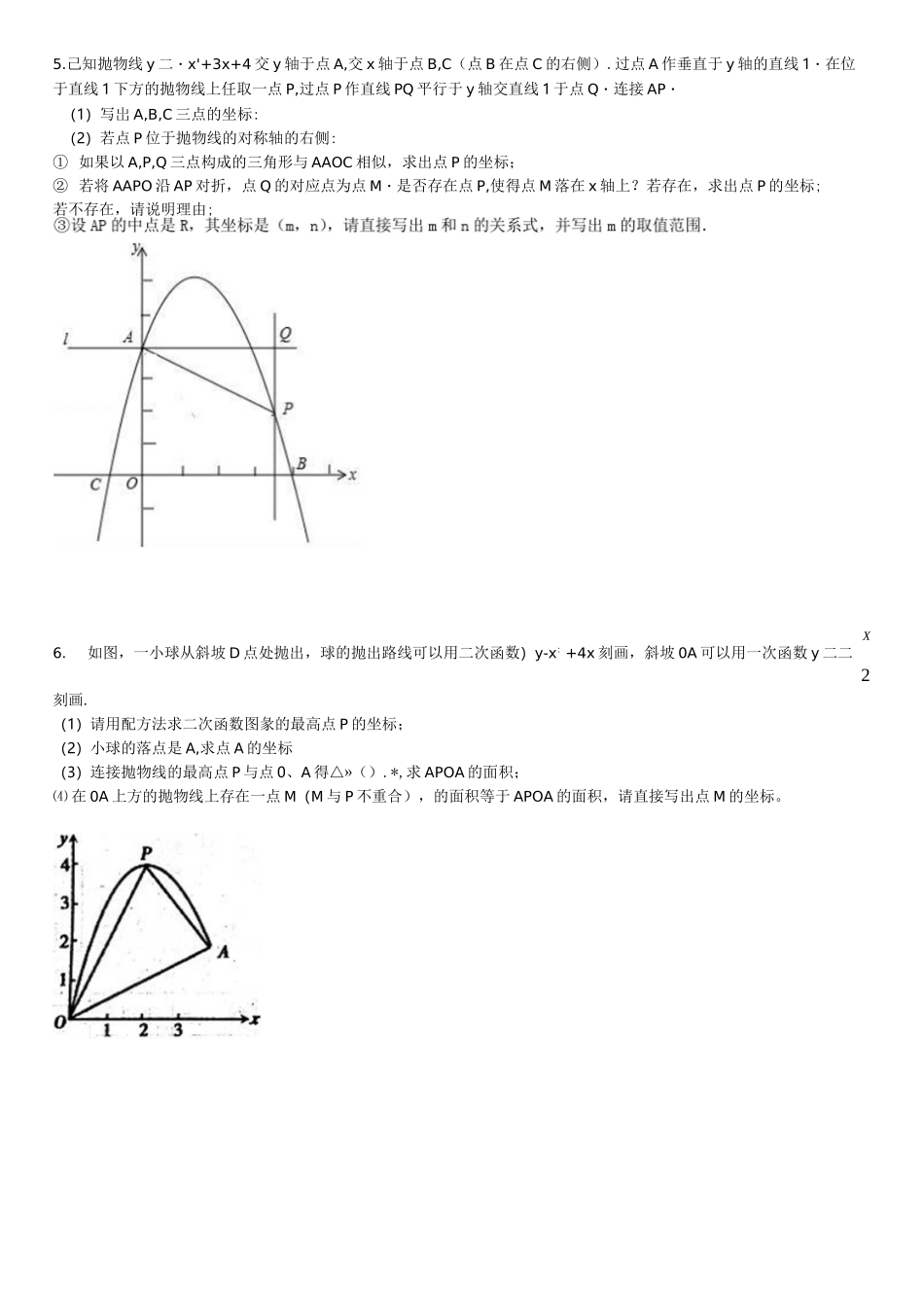
1.如图,抛物线y二ax'+bx+c(aHO)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x二1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;2.已知在平面直角坐标系xOy中,0是坐标原点,以P(1,1)为圆心的0P与x轴、y轴分别相切于点M和点N,点F从点H出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点P作PE丄PF交y轴于点E,设点F运动的时间是t秒(t>0)(1)若点E在y轴的负半轴上(如图所示),求证:PE二PF:(2)在点F运动过程中,设OE二a,OF二b,试用含a的代数式表示b:(3)作点F关于点M的对称点F',经过M、E和F'三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、0、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.333.如图1,已知抛物线y=8x:-4x-3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D(1)求出点A,B,D的坐标;(2)如图1,若线段0B在x轴上移动,且点0,B移动后的对应点为V,B'.首尾顺次连接点0,、B‘、D、C构成四边形O'B‘DC,请求出四边形0’B'DC的周长最小值.(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.4.如图,在RtAABC中,ZC=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为lcm/s,同时点Q从点B出发沿B-C-A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.(1)设点P的运动时间为x(秒),APBQ的面积为y(cm'),当APBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;(2)当x=5秒时,在直线PQ上是否存在一点M,使ABCH得周长最小,若存在,求出最小周长,若不存在,请说明理由.(3)当点Q在BC边上运动时,是否存在x,使得以APBQ的一个顶点为圆心作圆时,另外两个顶点均在这个圆上,若存在,求出x的值;不存在,说明理由.C5.己知抛物线y二・x'+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线1・在位于直线1下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线1于点Q・连接AP・(1)写岀A,B,C三点的坐标:(2)若点P位于抛物线的对称轴的右侧:①如果以A,P,Q三点构成的三角形与AAOC相似,求出点P的坐标;②若将AAPO沿AP对折,点Q的对应点为点M・是否存在点P,使得点M落在x轴上?若存在,求出点P的坐标;若不存在,请说明理由;X6.如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y-x:+4x刻画,斜坡0A可以用一次函数y二二2刻画.(1)请用配方法求二次函数图彖的最高点P的坐标;(2)小球的落点是A,求点A的坐标(3)连接抛物线的最高点P与点0、A得△»().*,求APOA的面积;⑷在0A上方的抛物线上存在一点M(M与P不重合),的面积等于APOA的面积,请直接写出点M的坐标。7.如图,己知二次函数Li:y=ax2-2ax+a+3(a>0)和二次函数L=:y=-a(x+1)2+l(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y二ax'-2ax+a+3(a>0)的最小值为_,当二次函数Li,L:的y值同时随着x的增大而减小时,x的取值范围是(2)当EF二MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).(3)若二次函数L:的图象与x轴的右交点为A(m,0),当AAMN为等腰三角形时,求方程-a(x+1)‘+1二0的解.8.已知直线y=kx+l经过点M(d,-2)和点N(1,2),交y轴于点H,交x轴于点F.(1)求d的值;(2)将直线MN绕点H顺时针旋转45°得到直线ME,点Q(3,e)在直线ME上,①证明ME〃x轴:②试求过H、N、Q三点的抛物线的解析式;(3)在(2)的条件卞,连接NQ,作△NMQ的高NB,点A为MN上的一个动点,若BA将△NMQ的面积分为1:2两部分,且射线BA交过M、N、Q三点的抛物线于点C,试求点C的坐标.4229.如图,在平面直角坐标系xOy中,抛物线y二X+C与直线y=--x«-交于A、B两点,已知点B的横坐5552?标是4,直线y=--X--与x、y轴的交点分别为A.C,点P是抛物线上一动点.55(1)求抛物线的解析式;22(2)若...