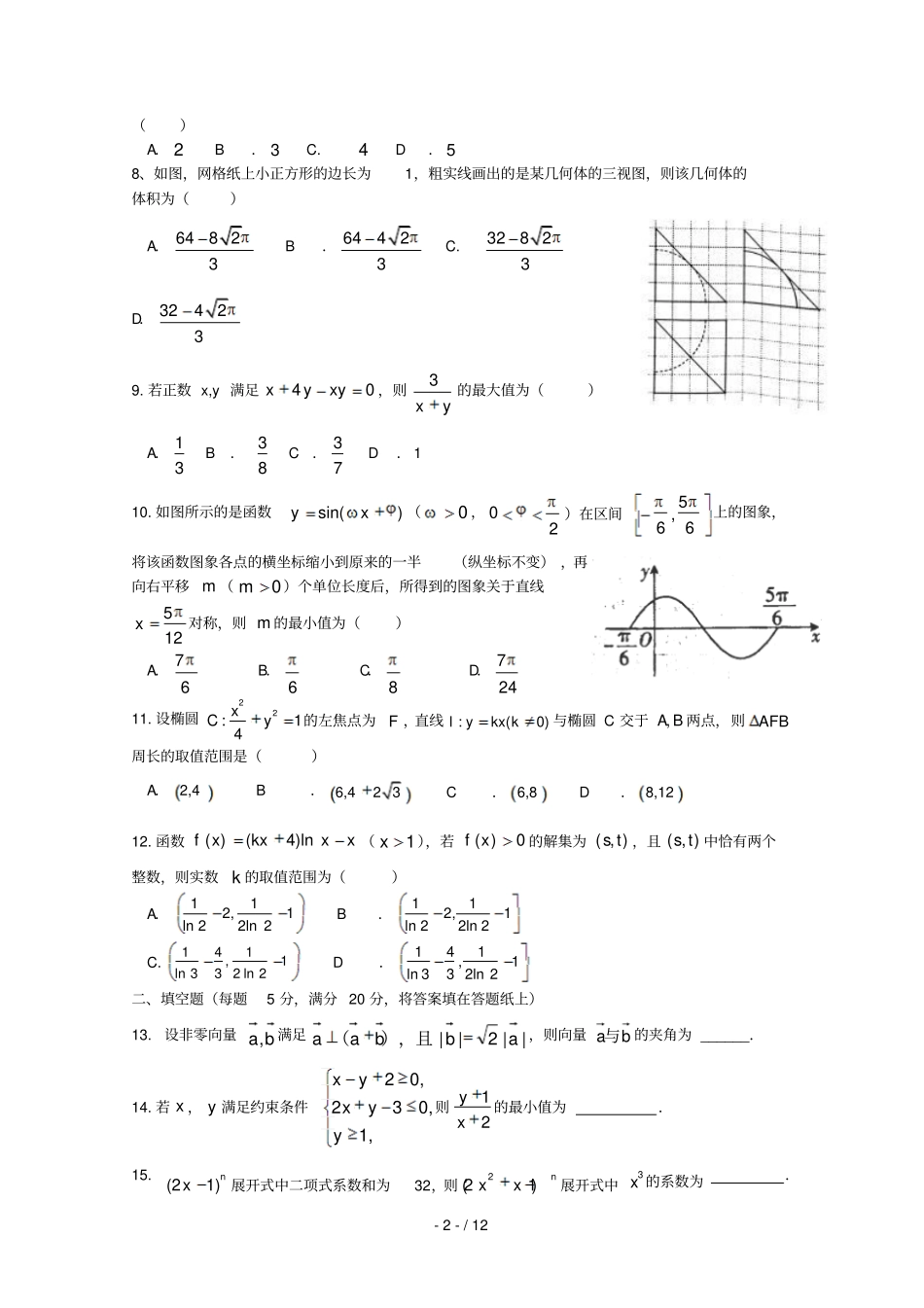
-1-/12广东省汕头市达濠华侨中学东厦中学2019届高三数学上学期第二次联考试题理一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合|24Axx,,则()A.|25xxB.|45xxx或C.|23xxD.|25xxx或2.复数22(1)1zii,则z=()A.13iB.12iC.12iD.13i3.设等差数列na的前项和为nS,若1033,12,7aSa则()A.10B.28C.30D.1454.若1cos()23,则cos(2)()A.79B.79C.429D.4295.右图是一个边长为4的正方形二维码,为了测算图中黑色部分的面积,在正方形区域内随机投掷400个点,其中落入黑色部分的有225个点,据此可估计黑色部分的面积为()A.11B.10C.9D.86.下面四个命题:1p:命题“2,2nnNn”的否定是“0200,2nnNn”;2p:向量,1,1,ambn,则mn是ab的充分且必要条件;3p:“在ABC中,若AB,则“sinsinAB”的逆否命题是“在ABC中,若sinsinAB,则“AB”;4p:若“pq”是假命题,则p是假命题.其中为真命题的个数是()A.1B.2C.3D.47.如下图所示的程序框图中,Mod,mn表示m除以n所得的余数,例如:Mod5,21,则该程序框图的输出结果为-2-/12()A.2B.3C.4D.58、如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A.64823B.64423C.32823D.324239.若正数x,y满足04xyyx,则yx3的最大值为()A.31B.83C.73D.110.如图所示的是函数sin()yx(0,02)在区间5,66上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移m(0m)个单位长度后,所得到的图象关于直线512x对称,则m的最小值为()A.76B.6C.8D.72411.设椭圆22:14xCy的左焦点为F,直线:(0)lykxk与椭圆C交于,AB两点,则AFB周长的取值范围是()A.2,4B.6,423C.6,8D.8,1212.函数()(4)lnfxkxxx(1x),若()0fx的解集为(,)st,且(,)st中恰有两个整数,则实数k的取值范围为()A.112,1ln22ln2B.112,1ln22ln2C.141,1ln332ln2D.141,1ln332ln2二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设非零向量ba,满足||2||abbaa),且(,则向量ba与的夹角为______.14.若x,y满足约束条件20,230,1,xyxyy则12yx的最小值为.15.(21)nx展开式中二项式系数和为32,则2(21)nxx展开式中3x的系数为.-3-/1216.已知数列中,,则数列的前项和为__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知的内角对边分别为a,b,c,满足.(1)求角;(2)若的外接圆半径为1,求的面积的最大值.18.已知等比数列na的前n项和为nS,且163nnSa(*nN).(1)求a的值及数列na的通项公式;(2)若nnnaanb23log)13(,求数列nb的前n项和nT.19.如图,四棱锥PABCD中,底面ABCD是直角梯形,90DAB,//ADBC,PAB是等边三角形,2DAAB,22PD,12BCAD,E为线段AB中点.(1)求证:平面PAB平面ABCD;(2)求二面角APDE余弦值.20.某体育公司对最近6个月内的市场占有率进行了统计,结果如表:(1)可用线性回归模型拟合与之间的关系吗?如果能,请求出关于的线性回归方程,如果不能,请说明理由;(2)公司决定再采购,两款车扩大市场,,两款车各100辆的资料如表:平均每辆车每年可为公司带来收入500元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命都是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的期望值作为决策依据,应选择采购哪款车型?参考数据:,-4-/12,,.参考公式:相关系数niniiiniiiyyxxyyxxr11221)()())((;回归直线方程,其中121()()niiiniixxyybxx,aybx21.已知函数2()ln1afxxx,aR.(1)讨论函数()fx的单调性;(2)设函数()()fxgxx,若()gx在21,e上存在极值,求a的取值范围,并判断极值的正负.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程已知曲线的极坐标方程是,以极点为平面直角坐标系的原点,极轴为轴的正半轴,建立平面直角坐标系,直线l的参数方程是(是参数),(Ⅰ)写出直线的普通方程和曲线的直角坐标方程;(Ⅱ)设曲线经过伸缩变换得到曲线,曲线任一点为,求点直线l的距离...