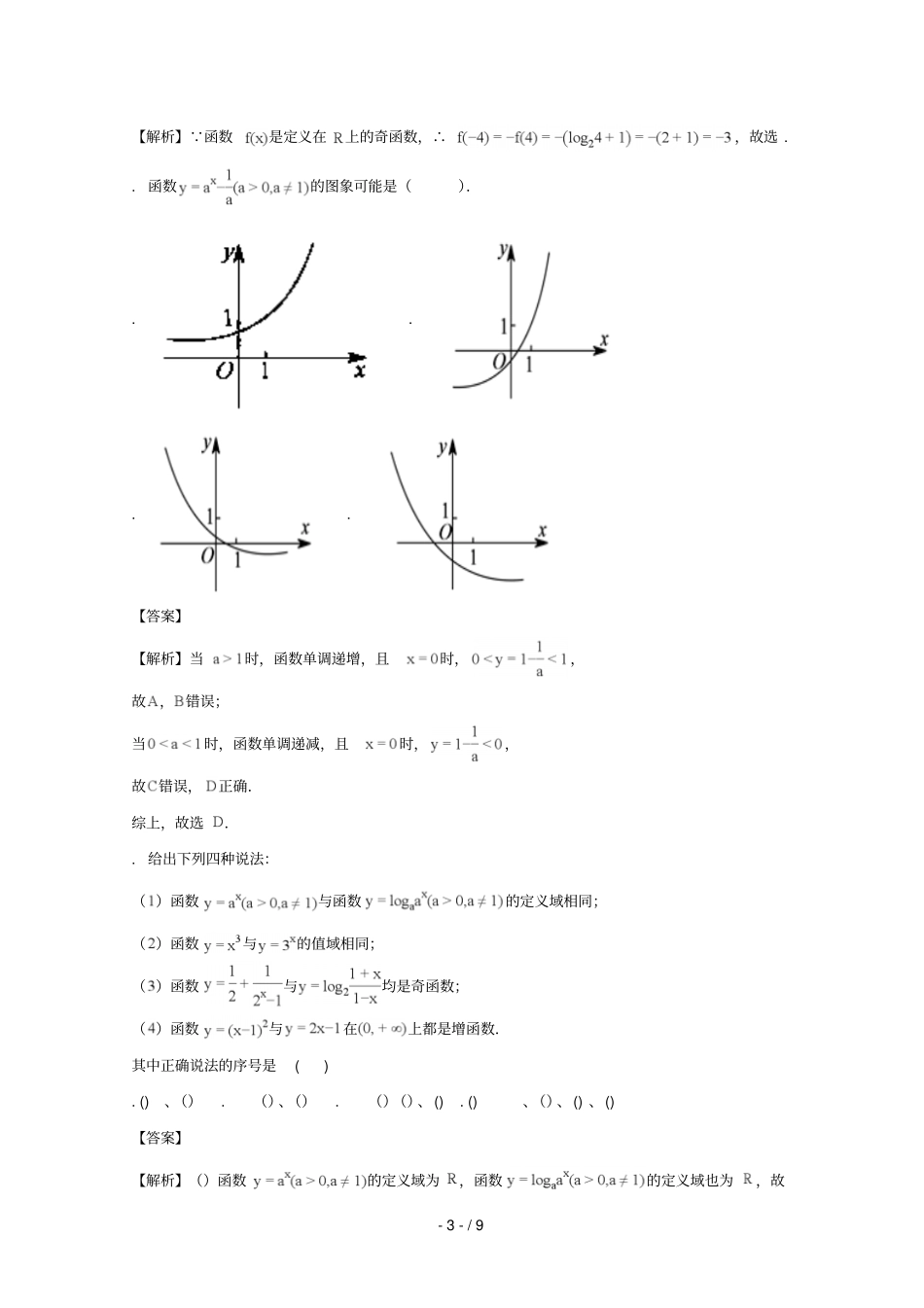
-1-/9南沙一中学年第一学期期中考试高一数学试题一、选择题(本大题共小题,每小题分,共分,在每小题给出的四个选项中,只有一项是符合题目要求的).若集合{,,},则下面结论中正确的是()....【答案】【解析】根据元素与集合之间是属于、不属于的关系,集合与集合之间为包含和包含于的关系可得:,故选..已知全集,,则()....【答案】【解析】 全集,集合,∴,故选..函数的定义域是().....【答案】【解析】要使函数有意义,则需,解得:,所以函数的定义域是:,故选..下列四个函数中,满足的函数是()....【答案】【解析】 不恒成立,∴选项不满足;恒成立,∴选项满足;不恒成立,∴选项不满足;不恒成立,∴选项不满足,故选..下列四组函数中,表示同一函数的一组是().,.,.,,,,.,【答案】【解析】对于,的定义域为,的定义域为,两者定义域不同,故不-2-/9合题意;对于:的定义域为,的定义域为,两者定义域不同,故不合题意;对于:两个函数的定义域分别为和,两者定义域不同,故不合题意;对于:由于,故两者为同一函数,故选.点睛:本题主要考查了判断两个函数是否为同一函数,属于基础题;函数的值域可由定义域和对应关系唯一确定;当且仅当定义域和对应关系均相同时才是同一函数,值得注意的是判断两个函数的对应关系是否相同,只要看对于定义域内任意一个相同的自变量的值,按照这两个对应关系算出的函数值是否相同..函数的单调递增区间是()....【答案】【解析】函数开口向上,对称轴是,函数在递增,故选..下列函数中,既是偶函数又在单调递增的函数是().....【答案】【解析】选项,是奇函数,故错误;选项,是偶函数,在上是减函数,故错误;选项,是偶函数,时,,所以在上是减函数,故错误,综上所述,故选..已知,,,则().....【答案】【解析】由于,,,则,故选..已知函数是定义在上的奇函数,当时,,则....【答案】-3-/9【解析】 函数是定义在上的奇函数,∴,故选..函数的图象可能是().....【答案】【解析】当时,函数单调递增,且时,,故,错误;当时,函数单调递减,且时,,故错误,正确.综上,故选..给出下列四种说法:()函数与函数的定义域相同;()函数与的值域相同;()函数与均是奇函数;()函数与在上都是增函数.其中正确说法的序号是().()、().()、().()()、().()、()、()、()【答案】【解析】()函数的定义域为,函数的定义域也为,故-4-/9正确;()函数的值域为,函数的值域为,故错误;()函数的定义域为, ,∴,故为奇函数;的定义域, ,∴,故其为奇函数,故()正确;()函数与在递减,函数在上递增,故错误;综上故选..已知是定义在上的奇函数,当时,,函数,如果对于任意,存在,使得,则实数的取值范围是().....【答案】【解析】 是定义在的奇函数,∴,当时,,∴当时,的值域为:; ,对称轴为:,∴,,即的值域为. 对于任意的,存在,便得,则且,即且,解得:,所以实数的取值范围是:,故选.二、填空题(本大题共小题,每小题分,共分).函数的定义域是。-5-/9【答案】【解析】要使函数有意义需满足,解得,故函数的定义域是,故答案为.点睛:本题主要考查了具体函数的定义域问题,属于基础题;常见的形式有:、分式函数分母不能为;、偶次根式下大于等于;、对数函数的真数部分大于;、的次方无意义;、对于正切函数,需满足等等,当同时出现时,取其交集..幂函数经过点(),则该幂函数的解析式是。【答案】【解析】设幂函数解析式为, 幂函数经过点,∴,解得,故该幂函数的解析式是:..已知集合,,则。【答案】【解析】由,得:,则,故答案为.点睛:首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.第二步常常是解一元二次不等式,我们首先用十字相乘法分解因式,求得不等式的解集.在解分式不等式的过程中,要注意分母不能为零.解指数或对数不等式要注意底数对单调性的影响.元素与集合之间是属于和不属于的关系,集合与集合间有包含关系.在求交集时注意区间端点的取舍.熟练画数轴来解交集、并集和补集的题目..已知函数。...