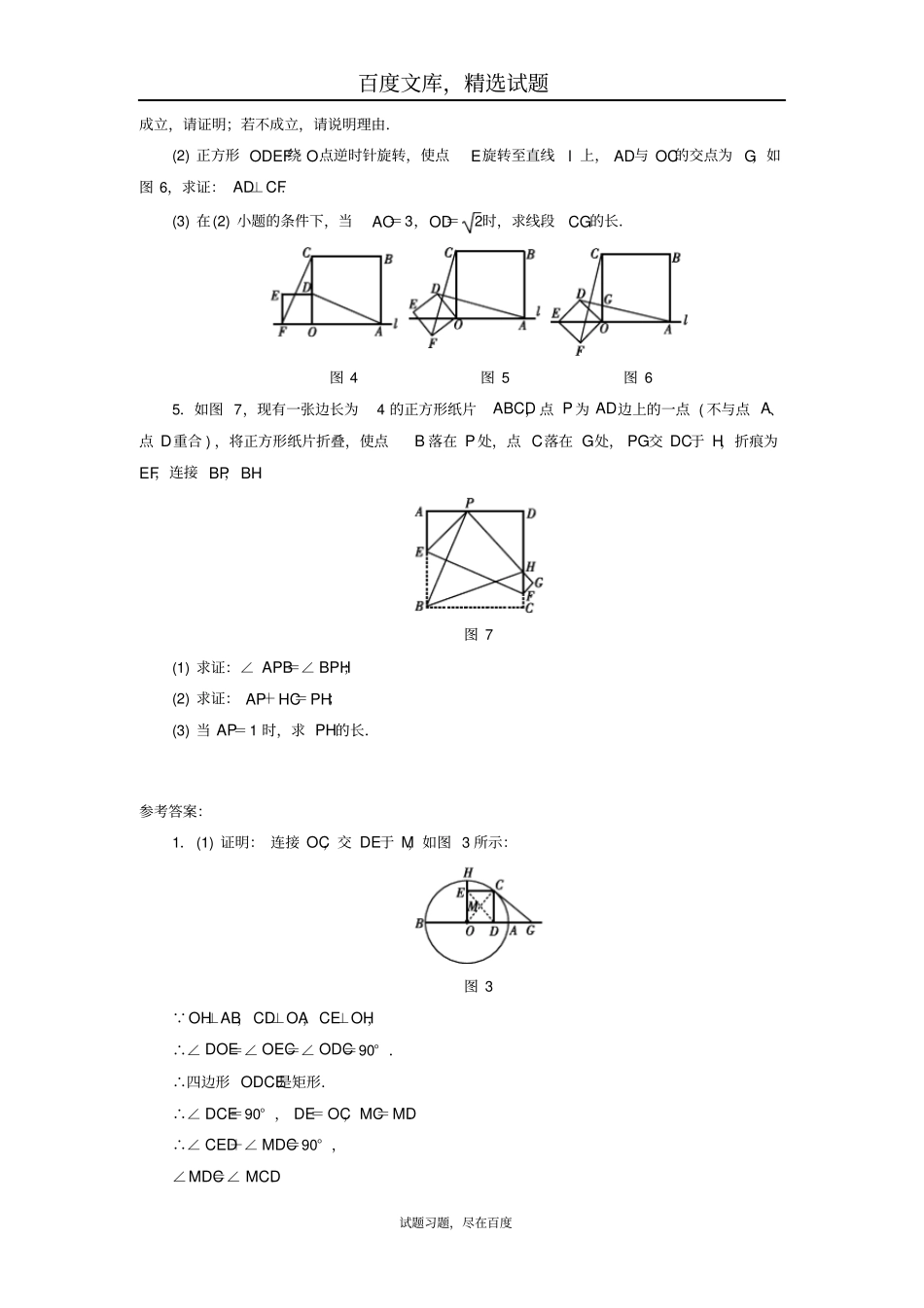
百度文库,精选试题试题习题,尽在百度专题训练九解答题突破——几何综合题1.如图1,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A,B的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D,E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.图1(1)求证:GC是⊙O的切线;(2)求DE的长;(3)过点C作CF⊥DE于点F,若∠CED=30°,求CF的长.2.如图2,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.图2(1)求证:BE=CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.3.(2016·丹东模拟)如图3,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.图3(1)∠ACB=__________°,理由是:________________________;(2)猜想△EAD的形状,并证明你的猜想;(3)若AB=8,AD=6,求BD.4.(2016·临沂模拟)如图4,正方形OABC与正方形ODEF放置在直线l上,连接AD,CF,此时AD=CF,AD⊥CF成立.(1)正方形ODEF绕O点逆时针旋转一定的角度,如图5,试判断AD与CF还相等吗?若百度文库,精选试题试题习题,尽在百度成立,请证明;若不成立,请说明理由.(2)正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,AD与OC的交点为G,如图6,求证:AD⊥CF.(3)在(2)小题的条件下,当AO=3,OD=2时,求线段CG的长.图4图5图65.如图7,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP,BH.图7(1)求证:∠APB=∠BPH;(2)求证:AP+HC=PH;(3)当AP=1时,求PH的长.参考答案:1.(1)证明:连接OC,交DE于M,如图3所示:图3 OH⊥AB,CD⊥OA,CE⊥OH,∴∠DOE=∠OEC=∠ODC=90°.∴四边形ODCE是矩形.∴∠DCE=90°,DE=OC,MC=MD.∴∠CED+∠MDC=90°,∠MDC=∠MCD.百度文库,精选试题试题习题,尽在百度 ∠GCD=∠CED,∴∠GCD+∠MCD=90°,即∠OCG=90°.∴GC⊥OC,点C是⊙O上一点,∴GC是⊙O的切线;(2)解:由(1)得:DE=OC=12AB=3;(3)解: ∠DCE=90°,∠CED=30°,∴CE=DE·cos∠CED=3×32=332.∴CF=12CE=334.1.(1)证明:连接OD,BD,图1 AB是⊙O的直径,∴AB⊥BC,即∠ABO=90°, AB=AD,∴∠ABD=∠ADB, OB=OD,∴∠DBO=∠BDO,∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°,∴AD是半圆O的切线;(2)证明:由(1)知,∠ADO=∠ABO=90°,∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD, AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°, BC是⊙O的直径,∴∠ODC+∠BDO=90°,∴∠BDO=∠CDE, ∠BDO=∠OBD,∴∠DOC=2∠BDO,∴∠DOC=2∠CDE,∴∠A=∠CDE;(3)解: ∠CDE=27°,百度文库,精选试题试题习题,尽在百度∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°, OB=2,∴BD的长=126·π×2180=75π.2.(1)证明: AD是直径,∴∠ABD=∠ACD=90°.在Rt△ABD和Rt△ACD中,AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD.∴∠BAD=∠CAD. AB=AC,∴BE=CE.(2)解:四边形BFCD是菱形.证明: AD是直径,AB=AC,∴AD⊥BC,BE=CE. CF∥BD,∴∠FCE=∠DBE.在△BED和△CEF中,∠FCE=∠DBE,BE=CE,∠BED=∠CEF=90°,∴△BED≌△CEF,∴CF=BD.∴四边形BFCD是平行四边形. ∠BAD=∠CAD,∴BD=CD.∴四边形BFCD是菱形.(3)解: AD是直径,AD⊥BC,BD=CD,∴∠AEC=∠CED=90°,∠CAE=∠DCE.∴△AEC∽△CED.∴ECED=AECE.∴CE2=DE·AE,设DE=x, BC=8,AD=10,∴42=x(10-x),解得:x=2或x=8(舍去)在Rt△CED中,CD=CE2+DE2=42+22=25.3.解:(1) AB是⊙O的直径,点C在⊙O上,∴∠ACB=90°(直径所对的圆周角是直角).(2)△EAD是等腰三角形.证明: ∠ABC的平分线与AC相交于点D,∴∠CBD=∠ABE. AE是⊙O的切线,∴∠EAB=90°.∴∠AEB+∠EBA=90°. ∠EDA=∠CDB,∠CDB+∠CBD=90°,百度文库,精选试题试题习题,尽在百度 ∠CBE=∠ABE,∴∠AED=∠EDA.∴AE=AD.∴△EAD是等腰三角形.(3)解:...