3、圆周运动的案例分析VIP免费

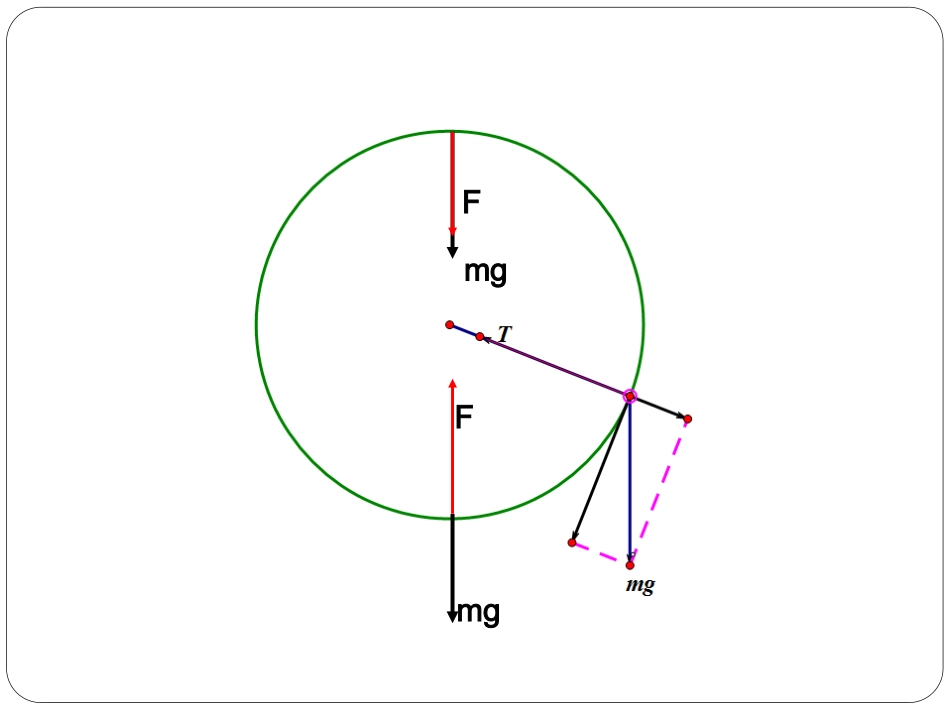
常见模型：轻绳、拱桥和轻杆模型考点1：最高点、最低点的受力特征考点2：最高点的临界速度的运用考点分析：mgFmgF一、轻绳模型：最高点：RvmmgF2小球恰能通过最高点临界条件：只受重力时，Rvmmg2临.gRv临即gR小球能过最高点：v≥二、拱桥模型：RvmFmgN2-最高点：物体m脱离轨道的临界条件是：轨道对物体m的支持力恰FN=0,即Rvmmg2临.gRv临即高点不脱离轨道的条件：gRv三、轻杆模型：最高点：RvmFmg2杆三、轻杆模型：最高点：RvmFmg2杆：0时，当.1杆FgRvRvmmg2的方向向下：时，当.2杆FgRvRvmFmg2杆的方向向上：时，当.3杆FgRvRvmFmg2杆杆mg时：0当.4Fv(此为小球能否过最高点的临界)【例题1】如图所示，2012年8月7日伦敦奥运会体操男子单杆决赛，荷兰选手宗德兰德荣获冠军，若他的质量为60kg,做“双臂大回环”用双手抓住单杆，伸展身体，以单杆为轴做圆周运动，此过程中，运动员到达最低点时手臂受的总拉力至少约为多少？（忽略空气阻力。g=10m/s2）()A.600NB.2400NC.3000ND.3600N当vmin=0m/s临界条件：RvmF2mg-）（2Rmgv21m212min2mvC过程：动能定理或机械能守恒定律状态：牛顿第二定律A.当两小环滑到同大环圆心等高时，大环对轻杆的拉力大小为MgB.当两小环滑到同大环圆心等高时，大环对轻杆的拉力大小为（2m+M）gC.两小环滑到大环底部时，大环对轻杆的拉力大小为2m（g+）+MgD.两小环滑到大环底部时，大环对轻杆的拉力大小为（2m+M）gRV2【练习1】如图所示，有一质量为M的光滑大圆环，半径为R，被一轻杆固定后悬挂在O点，有两个质量为m的小环（可视为质点）套在大环上，同时从大环两侧的对称位置由静止滑下，同时到达大环底部时速度为v，则（）mgN2mgN1mgTN1/N2/（1）为了使小球能通过甲轨道的最高点，试求A点离水平轨道的高度H至少为多少；【例题2】如图所示，半径为R=2m甲圆形轨道放置在竖直面内，斜面与水平轨道由一小段圆弧轨道相连，各段均光滑．现有一小球从光滑斜面上的A点由静止释放，那么：变式：为了使小球能不脱离甲轨道，试求A点离水平轨道的高度H的取值范围；（2）若小球以离地由静止从A点滑下，要使小球能滑上乙轨道而不脱离轨道，CD段的长度应满足什么条件？【例题2】如图所示，半径分别为R=2m和r=1m的甲、乙两圆形轨道放置在同一竖直面内，斜面与水平轨道由一小段圆弧轨道相连，两圆形轨道之间由一条水平轨道CD相连，小球与CD段间的动摩擦因数为μ=0.25，其余各段均光滑．现有一小球从光滑斜面上的A点由静止释放，那么：25R【练习2】如图所示，一小物块被夹子夹紧，夹子通过轻绳悬挂在小环上，小环套在水平光滑细杆上，物块质量为M，到小环的距离为L，其两侧面与夹子间的最大静摩擦力均为F.小环和物块以速度v向右匀速运动，小环碰到杆上的钉子P后立刻停止，物块向上摆动.整个过程中，物块在夹子中没有滑动.小环和夹子的质量均不计，重力加速度为g.下列说法正确的是A.物块向右匀速运动时，绳中的张力等于2FB.小环碰到钉子P时，绳中的张力大于2FC.物块上升的最大高度为D.速度v不能超过轻“绳”模型轻“杆”模型情景图示弹力特征弹力可能向下，也可能等于零弹力可能向下，可能向上，也可能等于零受力示意图临界特征FT＝0，即mg＝mv2r，得v＝grv＝0，即F向＝0，此时FN＝mgv＝gr的意义物体能否过最高点的临界点FN表现为拉力还是支持力的临界点拱桥模型弹力可能向上，也可能为0mgFN物体脱离轨道的临界点