《相似三角形的性质》VIP免费

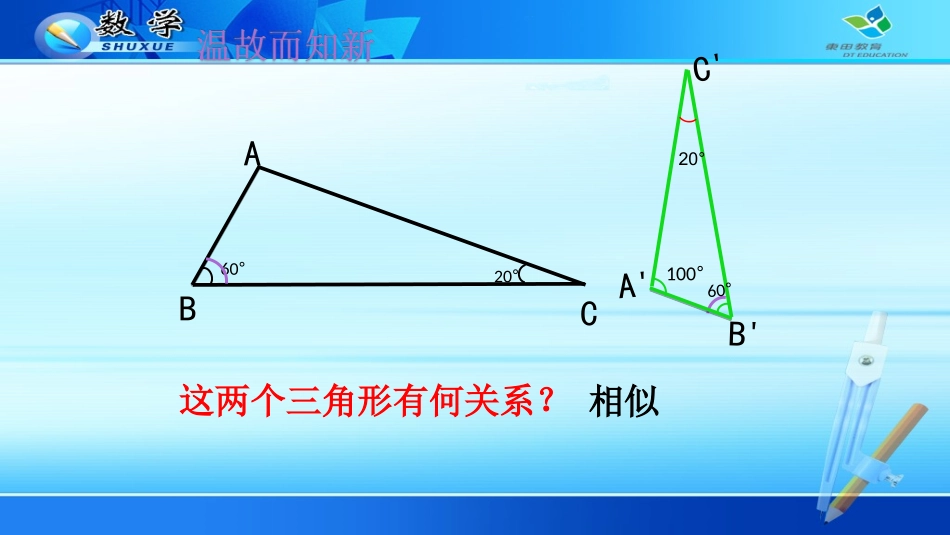
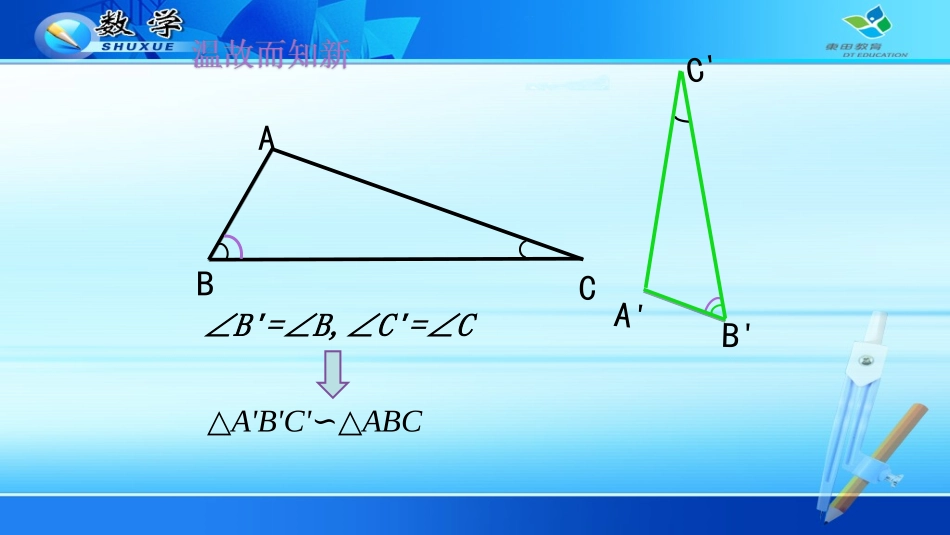
27.2.2相似三角形的性质B'A'C'100°60°A60°20°BC这两个三角形有何关系？相似20°B'A'C'ABC△A'B'C'ABC∽△∠B'=∠B,∠C'=∠CDABCD'B'A'(C')探究相似三角形对应边上的高之比与相似比有何关系?ADDA''?△A'B'C'ABC∽△ACCABCCBABBA''''''=kDABCD'B'A'(C')相似三角形的性质：相似三角形对应高的比等于相似比∵△A'B'C'ABC∽△RtA'D'C'RtADC△∽△=kADDAACCA''''kADDA''ACCABCCBABBA''''''相似三角形中，除了对应角、对应边、对应高外，还有哪些对应线段？对应角平分线、对应中线及周长DABCD'B'A'(C')角平分线FF'=kAFFAACCA''''△A'F'C'AFC∽△三角形中，除了角度和边长、高线外，还有哪些几何量？对应角平分线、对应中线及周长DABCD'B'A'(C')中线GG'=kAGGAACCA''''△A'G'C'AGC∽△相似三角形的性质：（1）相似三角形对应高的比都等于相似比.中线角平分线概括为：相似三角形所有对应线段之比都等于相似比.那么相似三角形周长的比与相似比有什么关系?（1）相似三角形对应高的比都等于相似比.中线角平分线概括为：相似三角形对应线段的比等于相似比.（2）相似三角形周长的比等于相似比kACBCABCACBBAkACBCABCkACkBBkAACBCABCACBBAllABCCBA)('''''''''''''''''''''相似三角形面积之比与相似比又有何关系？ABCCBASS'''ADBCDACB2121''''ADDABCCB''''kk相似三角形面积之比等于相似比的平方DABCD'B'A'(C')ABCCBASSk'''∟2k（1）相似三角形对应的比都等于相似比.相似三角形的性质:（3）相似三角形面积的比等于相似比的平方.（2）相似三角形周长的比等于相似比.高角平分线中线概括为：相似三角形对应线段的比等于相似比.1.已知两个三角形相似，请完成下列表格。相似比周长比面积比41610101004kkk2131319例3.如图:在△ABC和△DEF中AB=2DE,AC=2DF,∠A=∠D．若△ABC的边BC上的高为6，面积为,求△DEF的边EF上的高和面积.512CABDEF例3如图，在△ABC和△DEF中AB=2DE，AC=2DF,∠A=∠D．若△ABC的边BC上的高为6，面积为,求△DEF的边EF上的高和面积.CABDEF512解：在△ABC和△DEF中，∵AB=2DE，AC=2DF∴又∠D=∠A∴△DEF∽△ABC，△DEF与△ABC的相似比为，21ACDFABDE21512，3621∵△ABC的边BC上的高为6，面积为∴△DEF的边EF上的高为面积为53512212如图，在正方形网格上有△A1B1C1和△A2B2C2，高B2D2=。（1）求证：△A1B1C1A∽△2B2C2。（2）求：高B1D1的长；的面积比。510①②△A1B1C1和△A2B2C2（1）证明：在正方形网格中由勾股定理得:A1B1=,A2B2=222222112211CBCBBABA∵∠A1B1C1=∠A2B2C2=45°+90°=135°∴△A1B1C1∽△A2B2C2（2）解：①由上题可知：△A1B1C1与△A2B2C2的相似比为222211DBDB又∵B2D2=510∴B1D1=2×=5105102422222111CBACBASS②∵A1B1C1与△A2B2C2的相似比为2△1、相似三角形周长、对应高、对应中线、对应角平分线的比等于______。2、相似三角形面积的比等于__________。相似比相似比的平方3、化归与转化的数学思想、数形结合的数学思想方法及类比的方法。如图所示，D、E分别是AC、AB上的点，53ABADACAE，已知△ABC的面积为100㎝2，求四ABCDE1、必做：课本42页：6、7题2、选做：边形BCDE的面积。作业：