7.4.1二项式定理的证明VIP免费

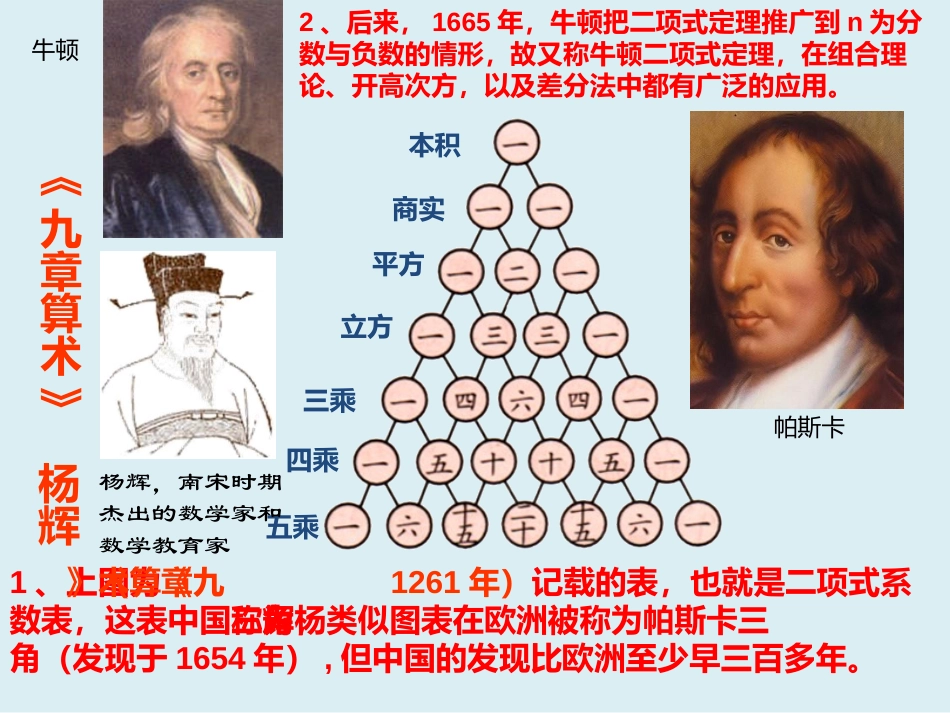
玉林实验中学朱丽平1、能用计数原理导出二项式定理；2、理解并掌握二项式定理及其通项公式，会用定理解决有关的简单问题.学习目标：《九章算术》杨辉1、上图为《九章算术》（1261年）记载的表，也就是二项式系数表，这表中国称为杨辉三角，类似图表在欧洲被称为帕斯卡三角（发现于1654年）,但中国的发现比欧洲至少早三百多年。本积平方立方三乘四乘五乘商实杨辉，南宋时期杰出的数学家和数学教育家2、后来，1665年，牛顿把二项式定理推广到n为分数与负数的情形，故又称牛顿二项式定理，在组合理论、开高次方，以及差分法中都有广泛的应用。牛顿帕斯卡1.两个盒子内各装有大小和质地相同的a,b两个小球，问在每个盒子中各取出一个球,共有几种不同的取法？你能用几种方法求解？ab02C12C22C2.三03C13C23C33Cabab2×2=4aaabbabb2、分步计数原理：1、列举法:3、分类计数原理：aabbabaaaaababbbbb取0个b取1个b取2个b取3个bab一、小题热身：问题问题2、请同学们尝试展开下列各式：二、推陈出新更新视角1)(baba222abab3)(ba2)(ba？100)(ba？nba)(322333babbaa……………….……………….(a+b)2＝(a+b)(a+b)弄清两个问题：1：展开后各项的类型有什么？类比取球数学模型重新分析(a+b)2展开式2：展开式中各项系数是什么，如何确定?a2，ab，b2(a+b)2＝(a+b)(a+b)1、展开后其项的形式为：a2，ab，b22、分析展开式中各项系数的情况：（考虑以b作为分类）（2）恰有1个取b的情况有C21种，则ab的系数为C21（3）恰有2个取b的情况有C22种，则b2的系数为C22（1）每个都不取b的情况有1种，即C20,则a2的系数为C20(a+b)2＝C20a2+C21ab+C22b2=a2+2ab+b22)、各项的系数是多少?a3a2bab2b31)、展开后各项的类型有什么？类比展开：(a+b)3＝(a+b)(a+b)(a+b)＝？恰有1个取b的情况有C31种，则a2b前的系数为C31恰有2个取b的情况有C32种，则ab2前的系数为C32恰有3个取b的情况有C33种，则b3前的系数为C33恰有0个取b的情况有C30种，则a3前的系数为C30(a+b)3=C30a3+C31a2b+C32ab2+C33b3＝a3+3a2b+3ab2+b3(a＋b)2＝a2＋2ab＋b2(a＋b)3＝a3＋3a2b＋3ab2＋b3＝a3＋a2b＋ab2＋b3(a＋b)4＝(a＋b)(a＋b)(a＋b)(a＋b)＝a4＋a3b＋a2b2＋ab3＋b40C3C31C32C33C44C40C41C42C43那么，(a＋b)n＝(a＋b)(a＋b)(a＋b)……(a＋b)=?三、水到渠成得出定理：Lnnbabababa)())(()(①项：②系数：kknba分析相乘个)(banaba中选个)(knbba中选个)(kknC0nC1nCnnCknC)()(*110NnbCbaCbaCaCbannnkknknnnnnn请分析的展开过程.nba)(LLnaban1kknbanb③展开式：取k个b二项式二项展开式1k记作:1knkkknTCab二项式定理：)(NnnnnkknknnnnnnbCbaCbaCaCba110)(这个公式叫做nab右边的多项式叫做二项式定理,左边的多项式叫做二项式,的二项展开式，其中各项的系数0,1,2knCkn称为二项式系数，式中的knkknCab展开式的第项,叫做二项展开式的通项，它是二项2.二项式系数规律：nnnnnCCCC、、、、2103.指数规律：（1）a的幂加b的幂等于n；（2）二项和的第一项a的次数由n逐次降到0，第二项b的次数由0逐次升到n.1.项数规律：展开式共有n+1个项定理特征：通项nnnkknknnnnnnbCbaCbaCaCba110思考：①二项展开式有多少项？为什么？②展开式的每一项系数如何，字母的指数如何变化？5432555445335225115005532808040101)2()2)2()2()2()2()21xxxxxxCxCxCxCxCxCx（解：（四、定理应用之初体验：例1求的二项展开式中相关问题.（1）展开式的第4项是多少？（2）展开式的第4项系数是多少？5)21(X项的系数指的是：二项式系数与数字系数的积。区分：二项式系数与项的系数的概念二项式系数指的是：knC333580)2(xxC1035C802335C（3）展开式的第4项二项式系数是多少？例2求二项式2x－1x6的展开式中常数项。解：由已知得二项展开式的通项为Tr＋1＝Cr6(2x)6－r·－1xr＝(－1)rCr6·26－r·x3－32r.∴令023...