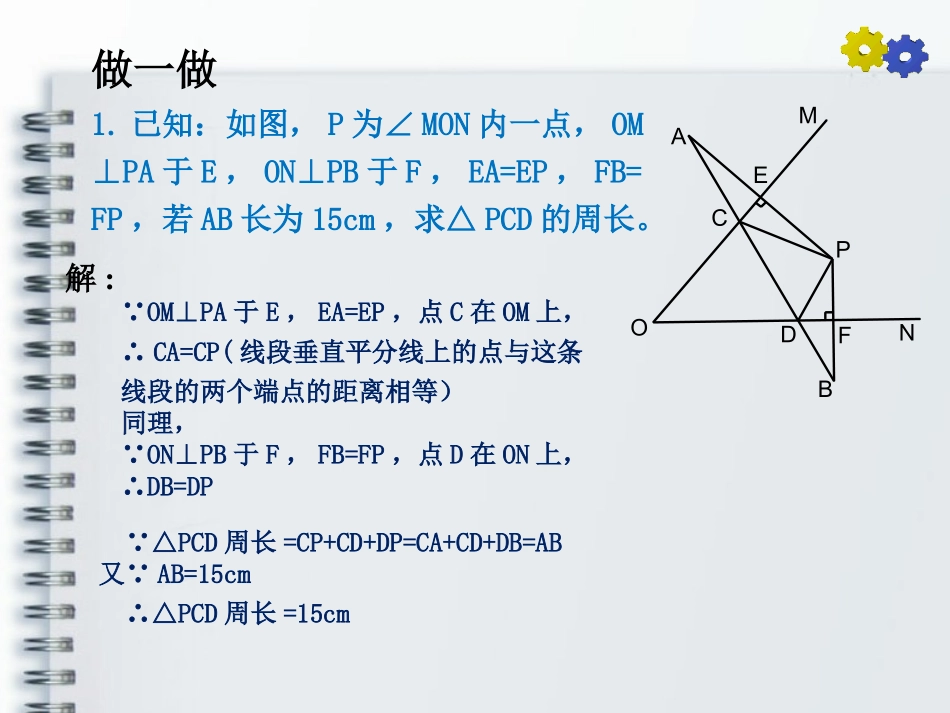
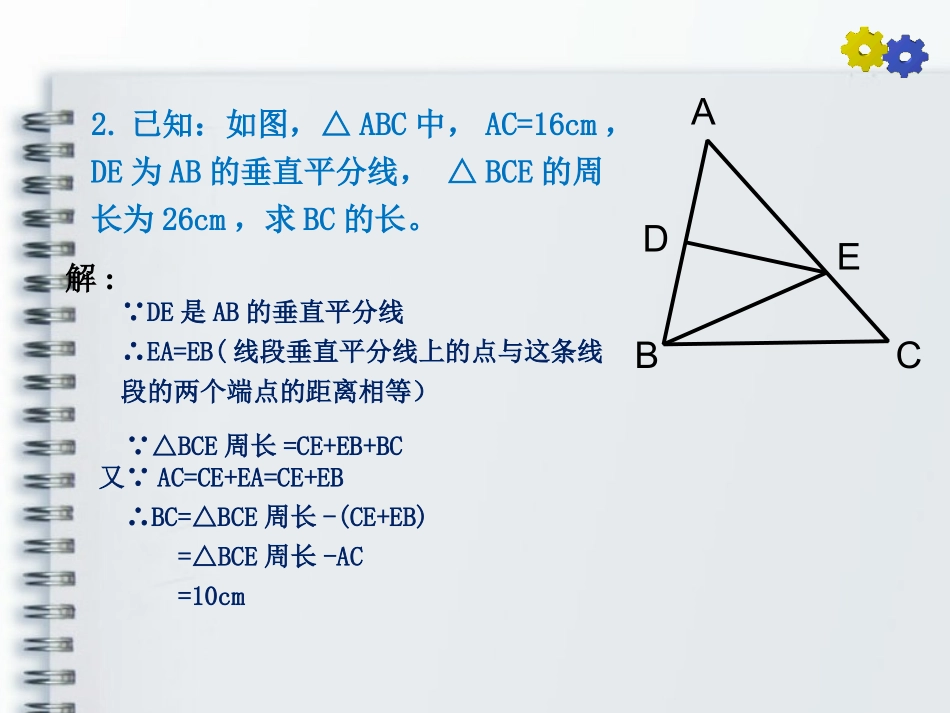
13.1.2线段的垂直平分线的性质课后练习解:做一做1.已知:如图,P为∠MON内一点,OM⊥PA于E,ON⊥PB于F,EA=EP,FB=FP,若AB长为15cm,求△PCD的周长。FENMODCBPA∵OM⊥PA于E,EA=EP,点C在OM上,∴CA=CP(线段垂直平分线上的点与这条线段的两个端点的距离相等)同理,∵ON⊥PB于F,FB=FP,点D在ON上,∴DB=DP∵△PCD周长=CP+CD+DP=CA+CD+DB=AB又∵AB=15cm∴△PCD周长=15cm2.已知:如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,求BC的长。EDCBA解:∵DE是AB的垂直平分线∴EA=EB(线段垂直平分线上的点与这条线段的两个端点的距离相等)∵△BCE周长=CE+EB+BC又∵AC=CE+EA=CE+EB∴BC=△BCE周长-(CE+EB)=△BCE周长-AC=10cm3.已知:如图,AC=AD,BC=BD,求证:AB垂直平分CD。∵AC=AD∴点A在CD的垂直平分线上()ODCBA证明:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上同理,∵BC=BD∴点B在CD的垂直平分线上∴AB垂直平分CD(两点确定一条直线)证明:如图作PC⊥AB则∠PCA=∠PCB=90°.在Rt△PCA和Rt△PCB中,∵PA=PB,PC=PC,∴Rt△PCA≌Rt△PCB(HL).∴AC=BC.又PC⊥AB,∴点P在线段AB的垂直平分线上PABC4.已知:如图,PA=PB.求证:点P在线段AB的垂直平分线上.解:∵AB=AC,∴点A在BC的垂直平分线.∵MB=MC,∵点M在BC的垂直平分线上∴直线AM是线段BC的垂直平分线.5.如图,AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?ABCDM