《相似三角形的性质》-(2)VIP免费

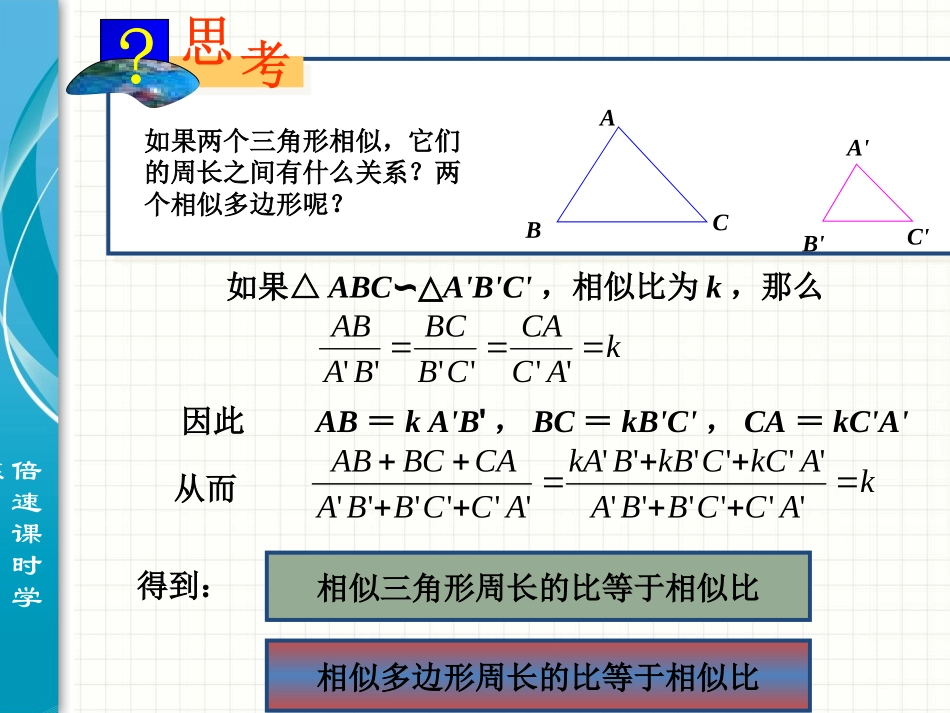
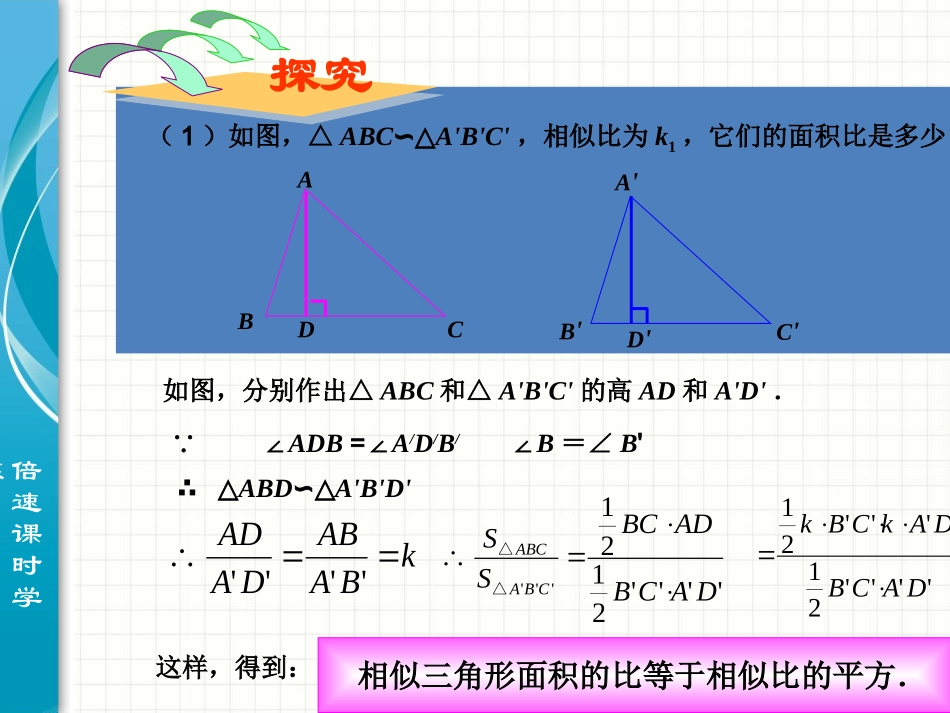
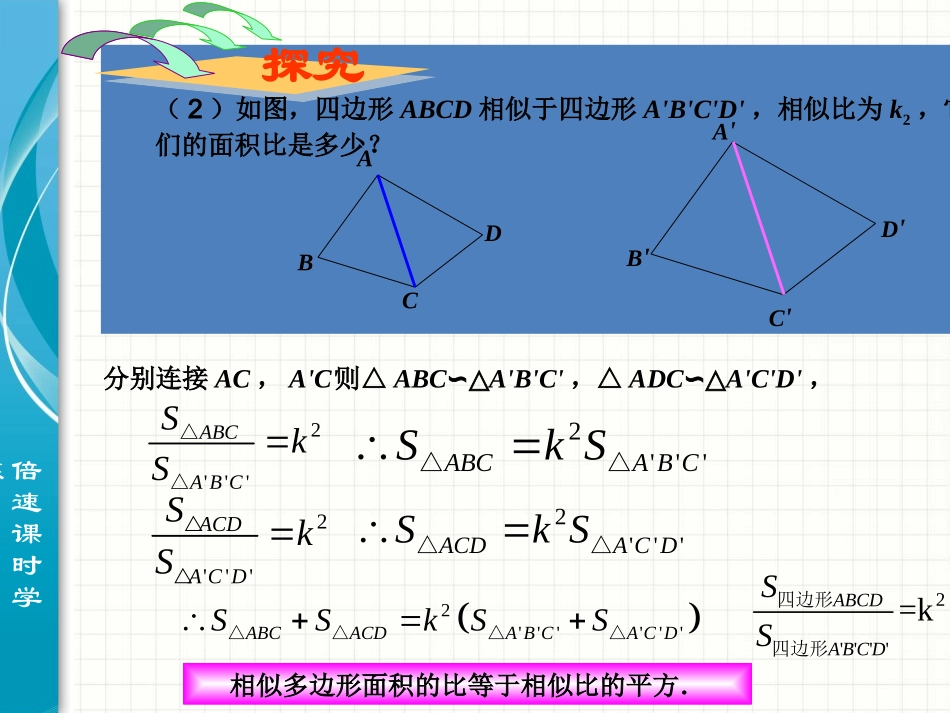
倍速课时学练如果两个三角形相似，它们的周长之间有什么关系？两个相似多边形呢？如果△ABC∽△A'B'C'，相似比为k，那么kACCACBBCBAAB''''''因此AB＝kA'B'，BC＝kB'C'，CA＝kC'A'从而kACCBBAAkCCkBBkAACCBBACABCAB''''''''''''''''''ABCA'B'C'相似多边形周长的比等于相似比得到：相似三角形周长的比等于相似比倍速课时学练探究（1）如图，△ABC∽△A'B'C'，相似比为k1，它们的面积比是多少？ABCA'B'C'D'D如图，分别作出△ABC和△A'B'C'的高AD和A'D'．∵∠ADB=∠A/D/B/∠B＝∠B'∴△ABD∽△A'B'D'kBAABDAAD''''''''2121'''DACBADBCSSCBAABC△△2''''21''''21kDACBDAkCBk这样，得到：相似三角形面积的比等于相似比的平方．倍速课时学练探究（2）如图，四边形ABCD相似于四边形A'B'C'D'，相似比为k2，它们的面积比是多少？ABCDA'B'C'D'则△ABC∽△A'B'C'，△ADC∽△A'C'D'，相似多边形面积的比等于相似比的平方．分别连接AC，A'C'2'''ABCABCSkS△△2'''ACDACDSkS2'''ABCABCSkS△△2'''ACDACDSkS△△2''''''ABCACDABCACDSSkSS△△△△2''''=kABCDABCDSS四边形四边形倍速课时学练例6.如图，在△ABC和△DEF中，AB＝2DE，AC＝2DF，∠A＝∠D，△ABC的周长是24，面积是48，求△DEF的周长和面积．解：在△ABC和△DEF中，∵AB＝2DE，AC＝2DF∴21ACDFABDE又∠D＝∠A∴△DEF∽△ABC，相似比为21ABCDEADE11,=L=122242ADEADEABCLLL△△△△11===124484ADEADEADEABCSSSS△△△△例题分析倍速课时学练1.判断（1）一个三角形的各边长扩大为原来的5倍，这个三角形的周长也扩大为原来的5倍；（2）一个四边形的各边长扩大为原来的9倍，这个四边形的面积也扩大为原来的9倍．练习解：（1）一个三角形各边扩大为原来5倍，相似比为1：5155原周长＝扩大倍周长扩大5倍周长＝5原周长倍速课时学练解：一个三角形各边扩大为原来9倍，相似比为1：92199SS原四边形＝扩大倍四边形边长扩大9倍四边形＝81倍原四边形的的面积（2）一个四边形的各边长扩大为原来的9倍，这个四边形的面积也扩大为原来的9倍．倍速课时学练2.如图，△ABC∽△A'B'C'，他们的周长分别为60cm和72cm，且AB=15cm，B'C'=24cm，求BC、AC、A'B'、A'C'的长．解：△ABC∽△A'B'C'60157218k15''18ABAB1818''15181515ABAB15''18BCBC15242018BC60152025AC''72182430ACABCA'B'C'倍速课时学练3.蛋糕店制作两种圆形蛋糕，一种半径是15cm,一种半径是30cm，如果半径是15cm的蛋糕够2个人吃，半径是30cm的蛋糕够多少人吃？（假设两种蛋糕高度相同）解：两地蛋糕是相似的相似比是1：2面积的比为211:42设半径是30cm的蛋糕够x人吃1：4＝2：xx=8答：半径是30cm的蛋糕够8个人吃．倍速课时学练4.在一张复印出来的纸上，一个多边形的一条边由原图中的2cm变成了6cm，这次复印的放缩比例是多少？这个多边形的面积发生了怎样的变化？6321解：放缩比例为面积发生了23911SS变化原图9SS变化原图