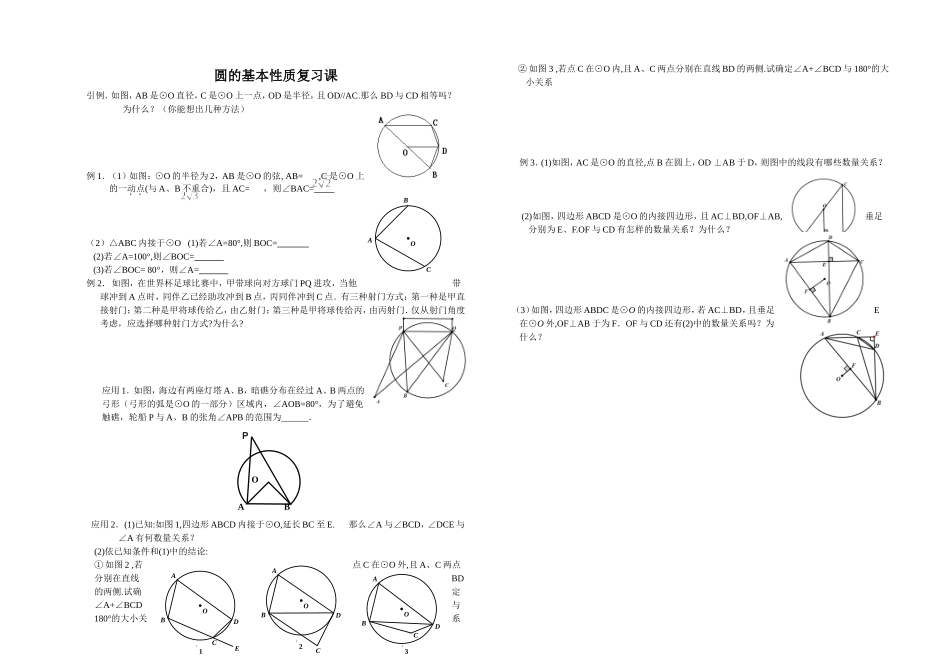
圆的基本性质复习课引例.如图,AB是⊙O直径,C是⊙O上一点,OD是半径,且OD//AC.那么BD与CD相等吗?为什么?(你能想出几种方法)例1.(1)如图:⊙O的半径为2,AB是⊙O的弦,AB=,C是⊙O上的一动点(与A、B不重合),且AC=,则∠BAC=(2)△ABC内接于⊙O(1)若∠A=80°,则BOC=(2)若∠A=100°,则∠BOC=(3)若∠BOC=80°,则∠A=例2.如图,在世界杯足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴乙已经助攻冲到B点,丙同伴冲到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门;第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择哪种射门方式?为什么?应用1.如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB的范围为______.应用2.(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.那么∠A与∠BCD,∠DCE与∠A有何数量关系?(2)依已知条件和(1)中的结论:①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系例3.(1)如图,AC是⊙O的直径,点B在圆上,OD⊥AB于D,则图中的线段有哪些数量关系?(2)如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥AB,垂足分别为E、F.OF与CD有怎样的数量关系?为什么?(3)如图,四边形ABDC是⊙O的内接四边形,若AC⊥BD,且垂足E在⊙O外,OF⊥AB于为F.OF与CD还有(2)中的数量关系吗?为什么?OCABABOPOC2BDA3COBDAOE1BDCA