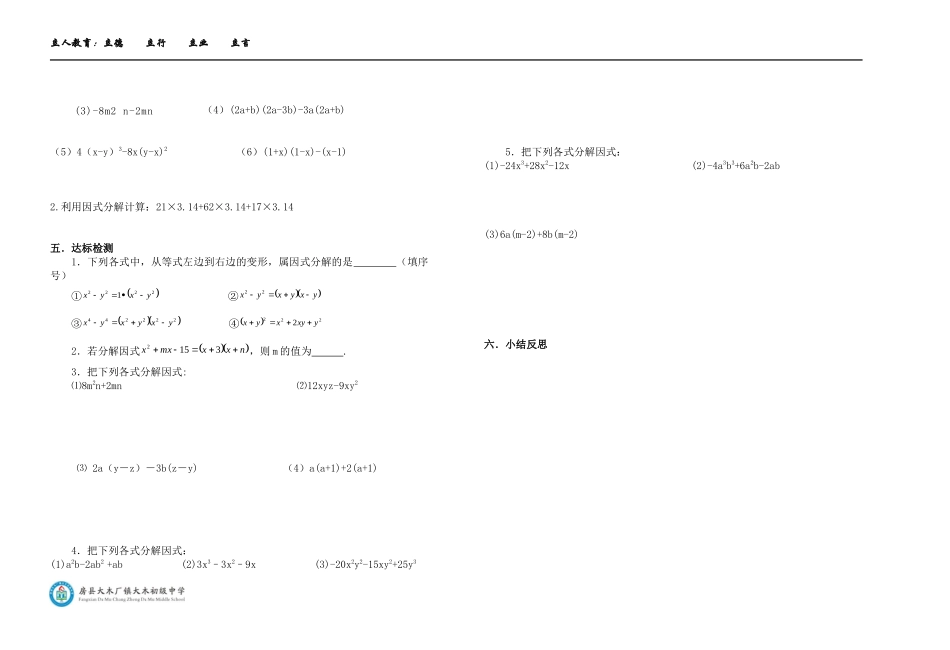
立人教育:立德立行立业立言大木初中导学案累计课时:22主备人:孙世莲时间:2016年10月17学习目标:1.了解因式分解的意义,并能够理解因式分解与多项式乘法的区别与联系.2.会用提公因式法进行因式分解.3.树立学生全面认识问题、分析问题的思想,提高学生的观察能力逆向思维能力.学习重点难点:掌握提取公因式,公式法进行因式分解导学过程:一、自主学习问题一:1.回忆:运用前两节所学的知识填空:(1)2(x+3)=___________________;(2)x2(3+x)=_________________;(3)m(a+b+c)=_______________________.2.探索:你会做下面的填空吗?(1)2x+6=()();(2)3x2+x3=()();(3)ma+mb+mc=()2.3.归纳:“回忆”的是已熟悉的运算,而要“探索”的问题,其过程正好与“回忆”,它是把一个多项式化为几个整式的乘积形式,这就是因式分解(也叫分解因式).4.反思:分解因式的对象是______________,结果是____________的形式.二、合作探究问题二:1.公因式的概念.⑴一块场地由三个矩形组成,这些矩形的长分别为a,b,c,宽都是m,用两个不同的代数式表示这块场地的面积.①_______________________________,②___________________________⑵填空:①多项式62x有项,每项都含有,是这个多项式的公因式.②3x2+x3有项,每项都含有,是这个多项式的公因式.③pa+pb+pc有项,每项都含有,是这个多项式的公因式.※多项式各项都含有的,叫做这个多项式各项的公因式.2.提公因式法分解因式.如果一个多项式的各项含有公因式,那么就可以,从而将多项式化成两个的乘积的形式,这种分解因式的方法叫做提公因式法.如ma+mb+mc=m(a+b+c)3.辨一辨:下列各式从左到右的变形,哪些是因式分解?(1)4a(a+2b)=4a2+8ab;()(2)6ax-3ax2=3ax(2-x);()(3)a2-4=(a+2)(a-2);()(4)x2-3x+2=x(x-3)+2.()(5)36ababa1232()(6)xabxabx()试一试:用提公因式法分解因式:(1)3x+6=3()(2)7x2-21x=7x()(3)24x3+12x2-28x=4x()(4)-8a3b2+12ab3c-ab=-ab()5.公因式的构成:①系数:各项系数的最大公约数;②字母:各项都含有的相同字母;③指数:相同字母的最低次幂.6.方法技巧:(1)、用提公因式法分解因式的一般步骤:a、确定公因式b、把公因式提到括号外面后,用原多项式除以公因式所得商作为另一个因式.(2)、为了检验分解因式的结果是否正确,可以用整式乘法运算来检验.问题三:1.把下列多项式分解因式:(1)(2)(3)(4)三.课堂练习:1.课本练习P115练习1,2,3题2.练一练:把下列各式分解因式:(1)ma+mb(2)5y3-20y2(3)四.盘点提升1.把下列各式分解因式:(1)-4kx-8ky(2)-4x+2x2立人教育:立德立行立业立言(3)-8m2n-2mn(4)(2a+b)(2a-3b)-3a(2a+b)(5)4(x-y)3-8x(y-x)2(6)(1+x)(1-x)-(x-1)2.利用因式分解计算:21×3.14+62×3.14+17×3.14五.达标检测1.下列各式中,从等式左边到右边的变形,属因式分解的是(填序号)①22221yxyx②yxyxyx22③222244yxyxyx④2222yxyxyx2.若分解因式nxxmxx3152,则m的值为.3.把下列各式分解因式:⑴8m2n+2mn⑵12xyz-9xy2⑶2a(y-z)-3b(z-y)(4)a(a+1)+2(a+1)4.把下列各式分解因式:(1)a2b-2ab2+ab(2)3x3–3x2–9x(3)-20x2y2-15xy2+25y35.把下列各式分解因式:(1)-24x3+28x2-12x(2)-4a3b3+6a2b-2ab(3)6a(m-2)+8b(m-2)六.小结反思立人教育:立德立行立业立言大木初中导学案累计课时:23主备人:孙世莲时间:2016年10月18学习目标:1.经历用平方差公式法分解因式的探索过程,理解公式中字母的意义。2.会用平方差公式法对多项式进行因式分解。3.体会从正、逆两个方面认识和研究事物的方法学习重点难点:应用平方差公式分解因式;导学过程:一、自主学习(a+2)(a-2)=(-x+3)(-x-3)=(3a+2b)(3a-2b)=自学课本P116-117,完成下列问题。1.什么条件下可以用平方差公式进行因式分解?3.如何将多项式x2-1和9x2-4分解因式?二、合作探究1.你能像分解x2-1和9x2-4一样将下面的多项式分...