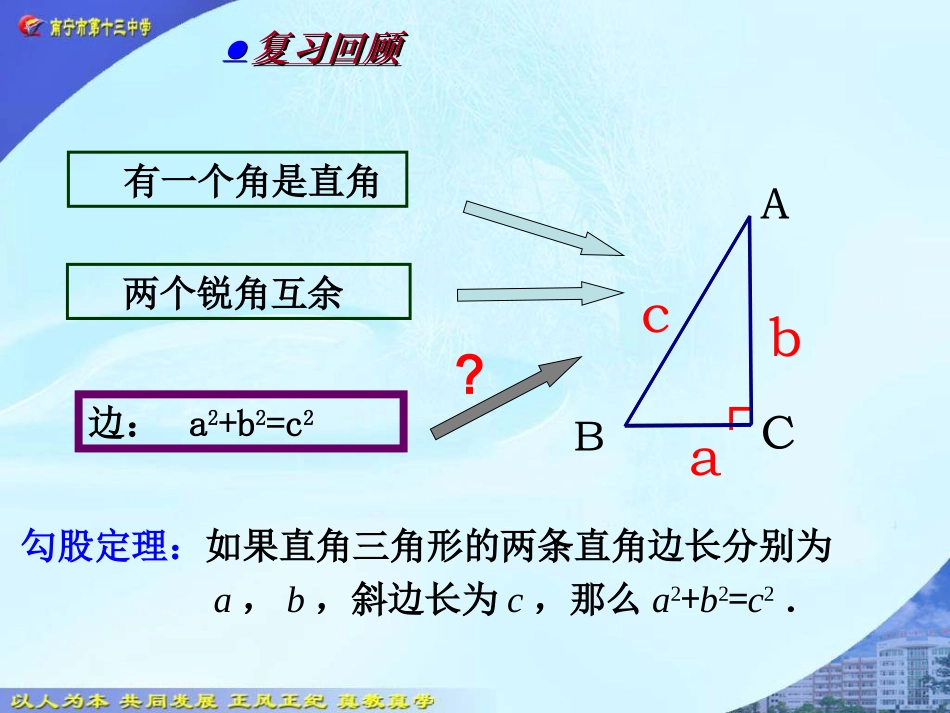
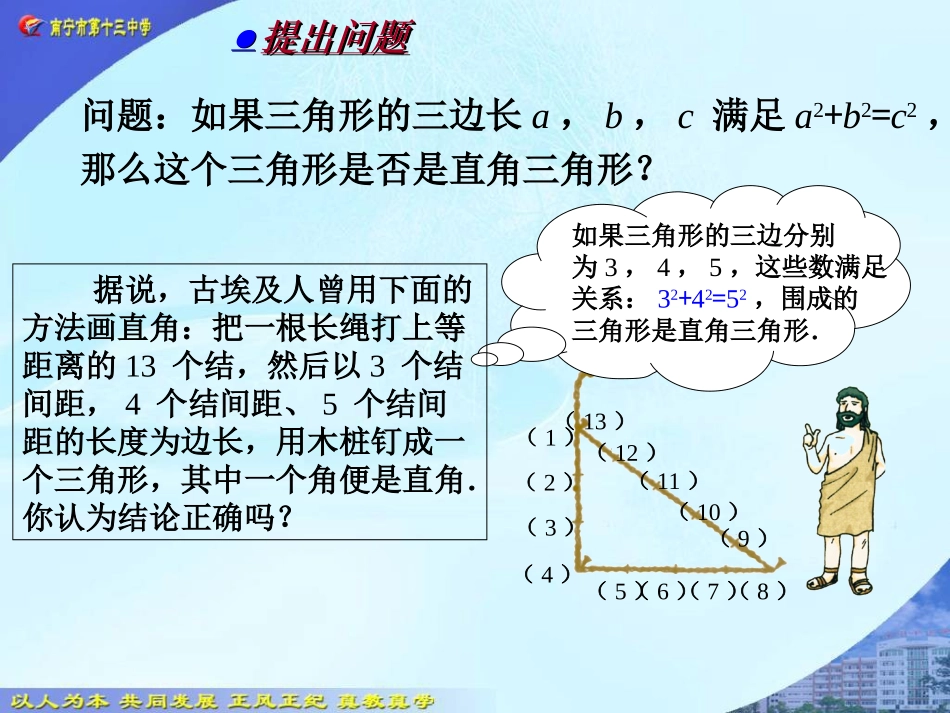
八年级下册17.2勾股定理的逆定理(1)南宁13中廖容清┏acbABC有一个角是直角两个锐角互余边:a2+b2=c2勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.?●●复习回顾复习回顾问题:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是否是直角三角形?(1)(2)(3)(4)(5)(6)(7)(8)(13)(12)(11)(10)(9)如果三角形的三边分别为3,4,5,这些数满足关系:32+42=52,围成的三角形是直角三角形.据说,古埃及人曾用下面的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你认为结论正确吗?●●提出问题提出问题实验操作:画一个△ABC,使它的三边长分别为:①2.5cm,6cm,6.5cm;②6cm,8cm,10cm.(1)这两个三角形的三边满足a2+b2=c2吗?(2)它们是直角三角形吗?如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.●●自主探究自主探究已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.求证:△ABC是直角三角形.?三角形全等∠C是直角△ABC是直角三角形ABCabc●●论证结论论证结论CABab已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.求证:△ABC是直角三角形.ABCabc●●论证结论论证结论CABab90'''''''''''''t'''''''t22222222CCABCCBAABcBAcBAcbabaBACBARbACCAaBCCBCBAR中,在,使得,证明:作定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.作用:判定一个三角形三边满足什么条件时为直角三角形.41例1判断由线段a,b,c组成的三角形是不是直角三角形:(1)a=15,b=17,c=8;(2)a=13,b=14,c=15;(3)a=,b=4,c=5.分析:用三边关系来判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.●●学以致用学以致用解:(1)∵152+82=225+64=289,172=289,∴152+82=172.∴以15,8,17为边长的三角形是直角三角形.41例1判断由线段a,b,c组成的三角形是不是直角三角形:(1)a=15,b=17,c=8;(2)a=13,b=14,c=15;(3)a=,b=4,c=5.像15,17,8这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.●●学以致用学以致用方法归纳:①找出最长边;②计算两条较短的边的平方和是否等于最长的边的平方。如果相等,则是直角三角形。最长边所对的角是直角。如果不相等,则不是直角三角形。勾股定理的逆定理:定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.勾股定理的逆命题:勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.●●知识归纳知识归纳观察:这两个命题的题设和结论有何关系?●●巩固练习巩固练习(1)两条直线平行,内错角相等.(2)如果两个实数相等,那么它们的绝对值相等.逆命题:内错角相等,两条直线平行.归纳:原命题成立时,逆命题有时成立,有时不成立成立不成立说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题:如果两个实数的绝对值相等,那么这两个实数相等.(1)勾股定理的逆定理的内容是什么?它有什么作用?(2)本节课我们学习了原命题,逆命题的知识,你能说出它们之间的关系吗?(3)在探究勾股定理的逆定理的过程中,我们经历了哪些过程?●●课堂小结课堂小结