三角形相似的条件2VIP免费

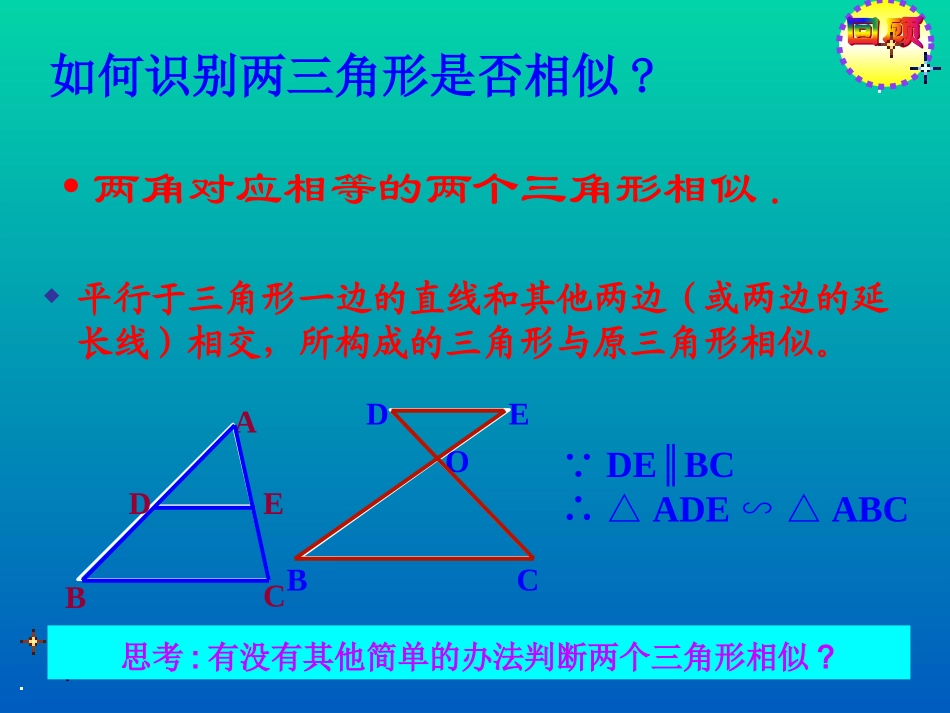
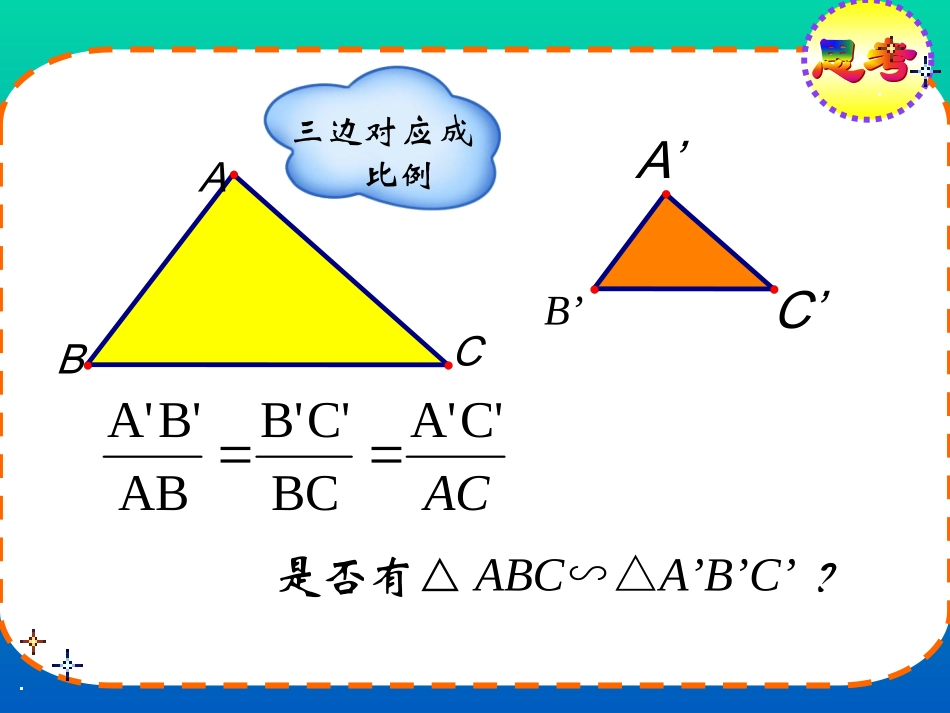
如何识别两三角形是否相似?∵DEBC∥∴△ADEABC∽△平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。DEOBCABCDE•两角对应相等的两个三角形相似.思考:有没有其他简单的办法判断两个三角形相似?ACC'A'BCC'B'ABB'A'是否有△ABC∽△A’B’C’？ABCC’B’A’三边对应成比例已知:如图△ABC和△A`B`C`中A`B`:AB=A`C`:AC=B`C`:BC.求证:ABCA`B`C`△∽△证明:在△ABC的边AB(或延长线)上截取AD=A`B`,A`B`C`ABCDE过点D作DE∥BC交AC于点E.又A`B`:AB=B`C`:BC=C`A`:CA∴△ADEABC∽△∴AD:AB=AE:AC=DE:BC,∵AD=A`B`∴AD:AB=A`B`:AB∴DE:BC=B`C`:BC,EA:CA=C`A`:CA.因此DE=B`C`,EA=C`A`.∴△A`B`C`∽△ABC∴△ADE≌△A`B`C`ABCC’B’A’ACC'A'BCC'B'ABB'A'△ABC∽△A’B’C’如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简单地说:三边对应成比例,两三角形相似.例1：在△ABC和△A′B′C′中，已知：(1)AB＝6cm，BC＝8cm，AC＝10cm，A′B′＝18cm，B′C′＝24cm，A′C′＝30cm．试判定△ABC与△A′B′C′是否相似，并说明理由．(2)AB=12cm，BC=24cm，AC＝15cmA’B’＝16cm，B’C’＝20cm，A’C’＝32cm，如图已知AEACDEBCADAB试说明∠BAD=∠CAE.ADCEBAEACDEBCADAB解∴ΔABC∽ΔADE∴∠BAC=∠DAE∴∠BAC━∠DAC=∠DAE━∠DAC即∠BAD=∠CAEDCBA如图，△ADE∽△ABC相似吗？ADAB？此时，A=AEAEAC=？3131如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形一定相似吗？•已知:如图△ABC和△A`B`C`中,A∠＝∠A`,,A`B`:AB=A`C`:AC.•求证:ABCA`B`C`△∽△A`B`C`ABCED证明:在△ABC的边AB上分别截取AD=A`B`,作DE//BC.A=A`,∠∠这样,ADEA`B`C`.△≌△相似三角形的判别∴△ABC∽△'''ABC如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。''''ABACABACA=A'ABCA′B′C′(两边对应成比例且夹角相等，两三角形相似)例2.判断图中△AEB和△FEC是否相似？1.ABCDEADBEACBCABCDCECDEC、如图，在中，，分别是和上的点，相似于吗？为什么？ABCDE2.在正方形ABCD中，E为AD上的中点,F是AB的四分一等分点，连结EF、EC；△AEF与△DCE是否相似?说明理由.ABCDFE3、已知：如图，BD、CE是△ABC的高，试说明△ADEABC∽△。ABCDE我思,我进步;5,1,2,AFEFAEAEF中在,22CEAE,2221EAEF.22105CAAF.CAAECEEFCEAE•如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.•解:AEFCEA.△∽△理由是:•设小正方形的边长是1,由勾股定理得;10,2,2,ACAECECEA中在∴△AEFCEA.∽△(三边对应边成比例的两个三角形相似.)ABCDEFGH平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;三边对应成比例的,两三角形相似.相似三角形的判定方法•两角对应相等的两个三角形相似.如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似ABCDEABCDE21OCBADOCDABABCDE