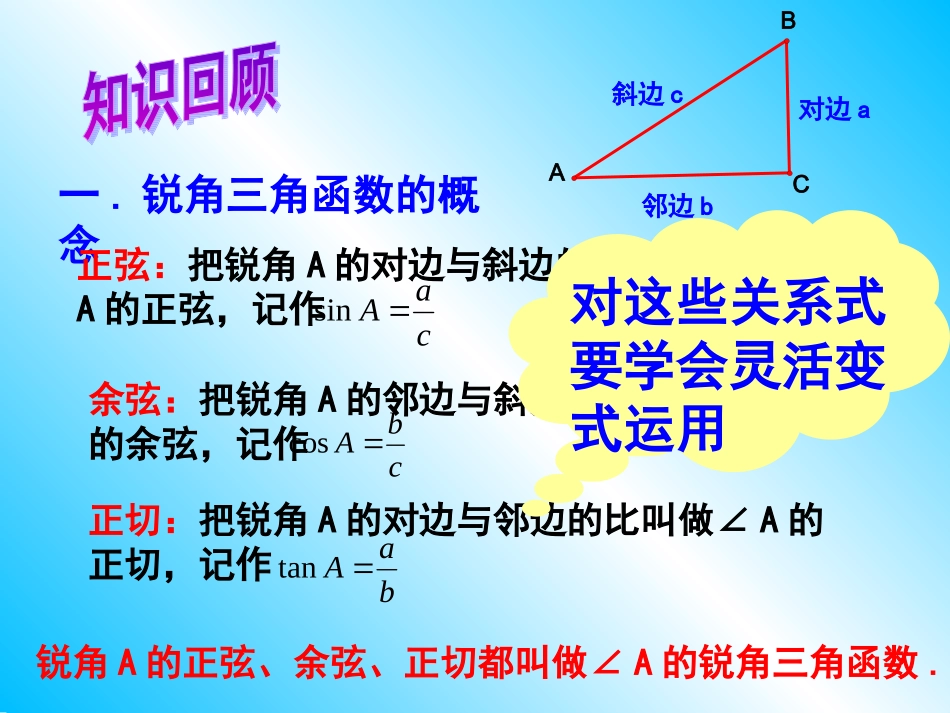
1.巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.2.熟记30°,45°,60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.4.会用解直角三角形的有关知识解决简单的实际问题.一.锐角三角函数的概念正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作caAsin余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作正切:把锐角A的对边与邻边的比叫做∠A的正切,记作cbAcosbaAtanBCA对边a邻边b斜边c锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.对这些关系式要学会灵活变式运用同一锐角的正弦值和余弦值之间的关系是:正弦值等于它的余角的余弦值,余弦值等于它的余角的正弦值.即sinA=cos(90°一A)=cosBcosA=sin(90°一A)=sinB思考:同一个锐角的正弦值和余弦值之间有何关系?二.特殊角的三角函数值2123222123223313锐角的三角函数值有何变化规律呢?三.解直角三角形由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.1.什么叫解直角三角形?2.直角三角形中的边角关系:222cba∠A十∠B=90°caAsincbAcosbaAtan归纳:只要知道其中的2个元素(至少有一个是边),就可以求出其余3个未知元素.(1)三边关系:(勾股定理)(2)两锐角的关系:(3)边角的关系:四.解直角三角形的应用1.仰角和俯角在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.铅直线水平线视线视线仰角俯角坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,则2.坡度、坡角坡角:坡面与水平面的夹角叫做坡角,用字母α表示.tanhilhltanhil坡度通常写成的形式.解:原式=2×+1×2121=1+21例1.计算2sin30°+tan45°×cos60°21=步骤:一“代”二“算”例2.若,则锐角α=01tan330°点拨:本题是由特殊角的三角函数值求角度,首先将原式变形为tanα=,从而求得α的度数.33例3.在Rt△ABC中,∠C=90°,∠A=30°,a=5,求b、c的大小.解: sinA=a/c,∴c=a/sinA=5/sin30=5/(1/2)=10.ABC530°∠B=90°-∠A=90°-30°=60°, tanB=b/a,∴b=a·tanB=5·tan60°=35解直角三角形分为两类:一是已知一边一角解直角三角形;二是已知两边解直角三角形.例4.如图,在△ABC中,AD是BC边上的高,若tanB=cos∠DAC.(1)AC与BD相等吗?说明理由;DCBA故BD=AC解:(1)在Rt△ABD和△ACD中,tanB=,=BDADACAD因为tanB=cos∠DAC,所以=BDADACADcos∠DAC(2)若sinC=,BC=12,求AD的长.1312例4.如图,在△ABC中,AD是BC边上的高,若tanB=cos∠DAC.(1)AC与BD相等吗?说明理由;DCBA(2)若sinC=,BC=12,求AD的长.1312(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,在Rt△ACD中,因为sinC=1312所以BC=18k=12,故k=32所以AD=12×=832.30cos260tan45sin22)1(200026tan303sin602cos45.1.若,则锐角α=02sin22.若,则锐角α=0320tan()3.计算:45°80°212214.如图,在Rt△ABC中,∠C=90,b=,c=4.则a=,∠B=,∠A=.32ABC260°30°D5.如果那么△ABC是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形03tan321cosBA例5.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.D分析:作PD⊥BC,设PD=x,则BD=x,AD=x+12,根据AD=PD,得x+12=x,求出x的值,再比较PD与18的大小关系.33解:有触礁危险.理由:过点P作PD⊥AC于D.设PD为x,在Rt△PBD中,∠PBD=90°-45°=45°.∴BD=PD=x,AD=12+x.在Rt△PAD中, ∠PAD=90°-60°=30°,,3PDAD∴渔船不改变航线继续向东航行,有触礁危险.,312xx.18)13(61312xD例6.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地...