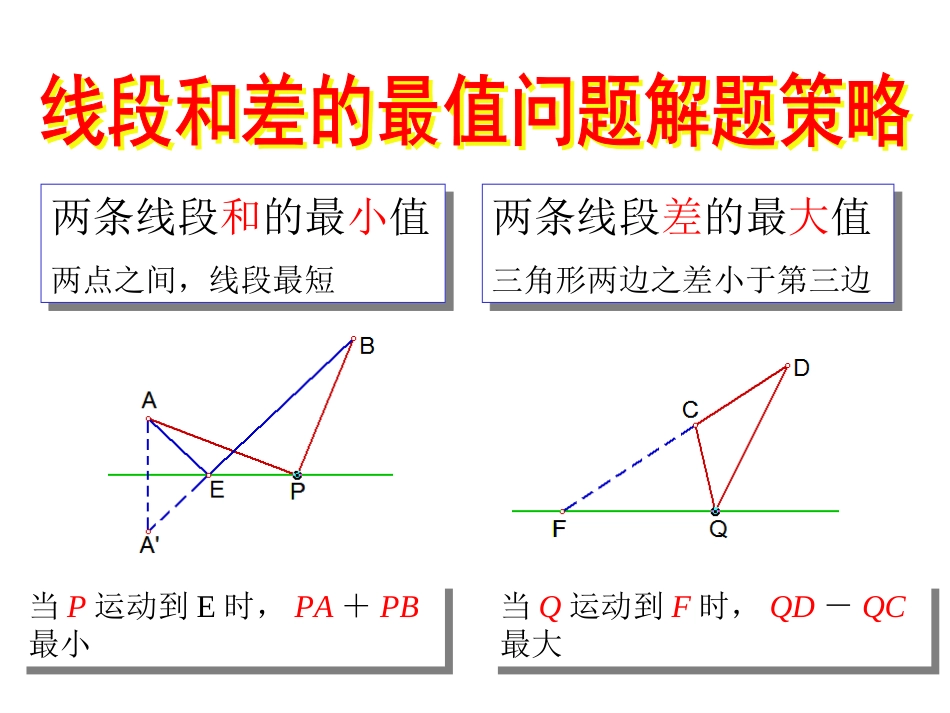
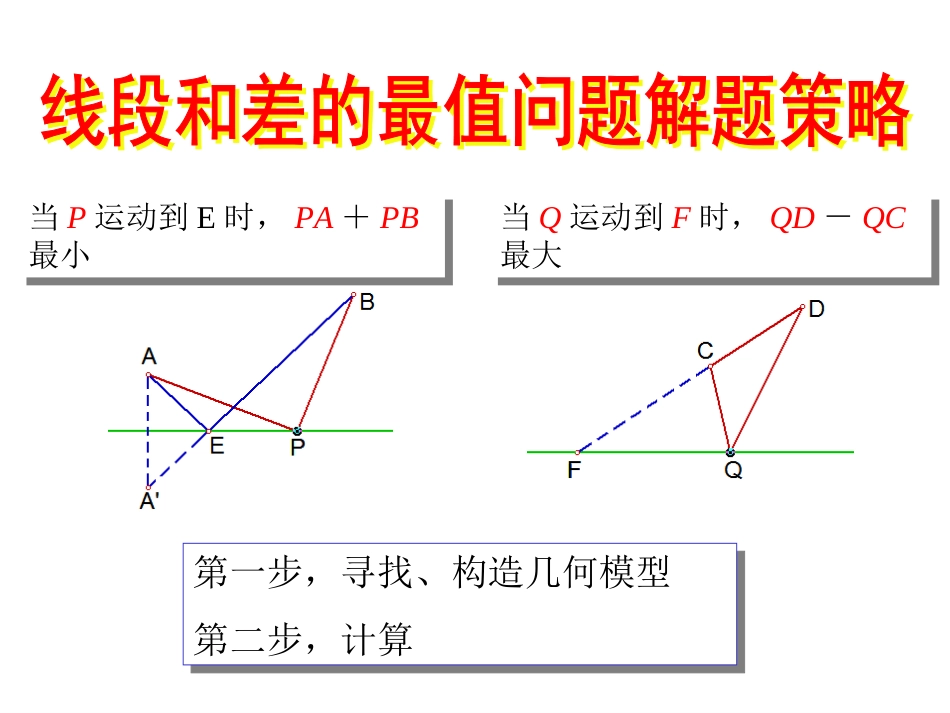
两条线段和的最小值两点之间,线段最短两条线段和的最小值两点之间,线段最短两条线段差的最大值三角形两边之差小于第三边两条线段差的最大值三角形两边之差小于第三边当P运动到E时,PA+PB最小当P运动到E时,PA+PB最小当Q运动到F时,QD-QC最大当Q运动到F时,QD-QC最大当P运动到E时,PA+PB最小当P运动到E时,PA+PB最小当Q运动到F时,QD-QC最大当Q运动到F时,QD-QC最大第一步,寻找、构造几何模型第二步,计算第一步,寻找、构造几何模型第二步,计算例1:在△ABC中,AC=BC=2,∠ACB=90O,D是BC边的中点,E是AB上的一动点,则EC+ED的最小值为。ACBDEp例2:△ABC中,AC=3,BC=4,AB=5,试在AB上找一点P,在BC上取一点M,使CP+PM的值最小,并求出这个最小值。ABCPMC/例1、例2中的最小值问题,所涉及到的路径,虽然都是由两条线段连接而成,但是路径中的动点与定点的个数不同,例1中的路径为“定点→动点→定点”,“定点→动点→定点”,是两个定点一个动点,而例2中的路径是“定“定点→动点→动点”,点→动点→动点”,是一个定点两个动点,所以两个题的解法有较大差异,例1是根据两点之间线段最短两点之间线段最短求动点的位置,例2是根据垂线段最短垂线段最短找两个动点的位置。例3:已知二次函数图像的顶点坐标为C(3,-2),且在x轴上截得的线段AB的长为4,在y轴上有一点P,使△APC的周长最小,求P点坐标。ACBA/OP例4:抛物线y=ax2+bx+c经过点A(-4,3),B(2,0),当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C(0,-2)的直线a与x轴平行。(1)求直线AB和抛物线,(2)设直线AB上点D的横坐标为-1,P(m,n)是抛物线上的一动点,当△POD的周长最小时,求P点坐标。ABOCDPABOCDP例例33,例,例44中最小值问题,所涉及到中最小值问题,所涉及到的路径虽然都是有两条动线段连接而的路径虽然都是有两条动线段连接而成,且路径都是成,且路径都是“定点→动点→定“定点→动点→定点”,点”,但是动点运动的路线不同,例但是动点运动的路线不同,例33是直线,例是直线,例44是曲线,因此它们的是曲线,因此它们的解法有很大不同,例解法有很大不同,例33是根据是根据两点之两点之间线段最短间线段最短找到动点的位置,例找到动点的位置,例44是是根据根据垂线段最短垂线段最短找到所求的两个动点找到所求的两个动点的位置。的位置。例5:在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.要求四边形MNFE的周长最小?要求四边形MNFE的周长最小?把三条线段转移到同一条直线上就好了!把三条线段转移到同一条直线上就好了!第一步第一步寻找、构造几何模型寻找、构造几何模型EFE/F/MN第二步计算——勾股定理543''22FE52122EF.55的周长的最小值为因此四边形MNFE.55的周长的最小值为因此四边形MNFE小结经典模型:台球两次碰壁问题经典模型:台球两次碰壁问题经验储存:没有经验,难有思路经验储存:没有经验,难有思路例6:在平面直角坐标系中,RtAOB△的顶点坐标分别是A(-2,0),O(0,0),B(0,4),把△AOB绕O点按顺时针旋转90度,得到△COD,(1)求C、D的坐标,(2)求经过A、B、D三点的抛物线。(3)在(2)中的抛物线的对称轴上取两点E、F(E在F点的上方),且EF=1,当四边形ACEF的周长最小时,求E、F的坐标。ABCEFDD/O例5、例6中的最小值问题所涉及到的路径,虽然都是由三条动线段连接而成,且路径都是“定点→动点→动点→定点”,但是例5中的量动点间的线段长度不确定,而例6的两动点间的线段长度为定值,正是由于这点的不同,使得它们的解题方法有很大差异,例例55是根据是根据两点之间线段最两点之间线段最短短找到动点的位置,例找到动点的位置,例66是通过是通过构造平行构造平行四边形四边形先找到所求的其中一个动点的位置,先找到所求的其中一个动点的位置,另一个位置也随之确定。另一个位置也随之确定。1、已知在对抛物线的对称轴上存在一点P,使得△PBC的周长最小,请求出点P的坐标.要求△PBC的周长最小?要求△PBC的周长最小?第一步寻找、构造几何模型只要PB+PC最小就...