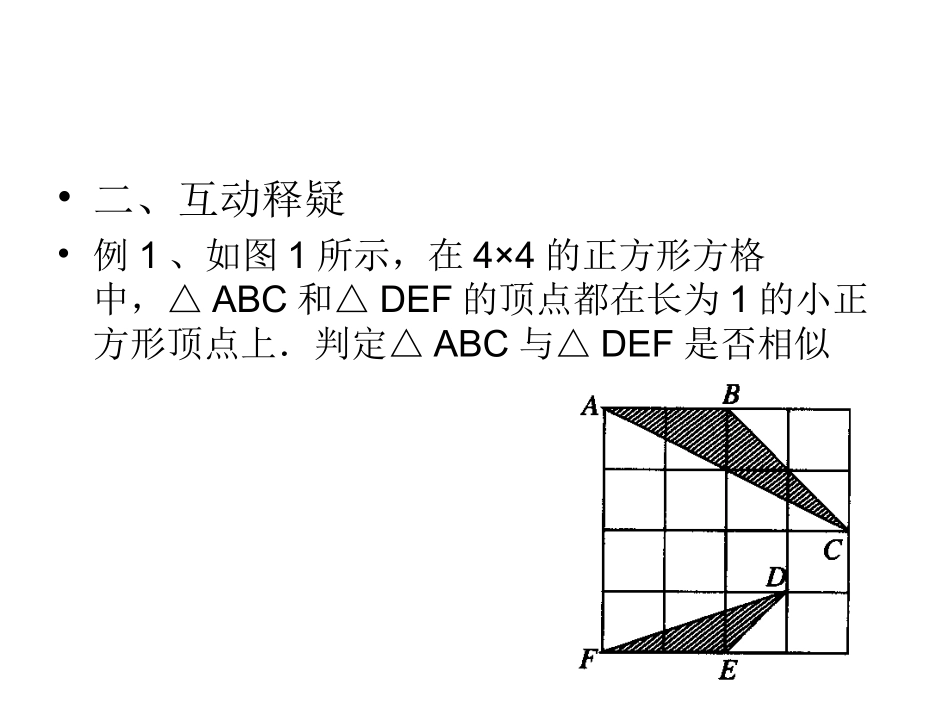
相似三角形一、自主探究1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形•4.相似三角形的基本性质•相似三角形的对应边成比例、对应角相等.•相似三角形的周长比等于相似比,面积比等于相似比的平方,相似三角形中对应线段的比等于相似比。•5.相似三角形的判定定理•①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;•②三边对应成比例的两个三角形相似;•③两角对应相等的两个三角形相似;•④两边对应成比例且夹角相等的两个三角形相似。•二、互动释疑•例1、如图1所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.判定△ABC与△DEF是否相似•例2、如图2所示,D、E两点分别在△ABC两条边上,且DE与BC不平行,请填上一个你认为适合的条件_________,使得△ADEABC∽△•例3、(2008年安徽省中考题)如图3,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q。•(1)请写出图中各对相似三角形(相似比为1除外);•(2)求BP∶PQ∶QR。图3QPRDECBA三、反馈拓展1、(2008年贵州省中考题)如图4,点D、E分别是等边三角形ABC的BC、AC边上的点,且BD=CE,AD与BE相交于点F,BD2=AD·DF吗?为什么?图4FEDCBA2.(2008年北京市中考题)如图5,己知:在RTABC△中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A,若ADAO∶=85∶,BC=2,求BD的长。3、(2008年福州市中考题)如图6,己知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P的运动速度是1cm/s,点Q的运动速度是2cm/s,当Q点到达点C时,P、Q两点都停止运动,设运动时间为t(s),作QRBA∥交AC于点R,连接PR,当t为何值时,△APRPRQ∽△?图6BQPCRA4、(2008年上海市中考题)已知AB=2,AD=4,∠DAB=90,ADBC∥(如图7)。E是射线BC上的动点,(点E与点B不重合),M是线段DE的中点。连接BD,交线段AM于点N,如果以A、N、D为顶点的三角形与△BME相似,求线段BE的长。图7MEDCBA