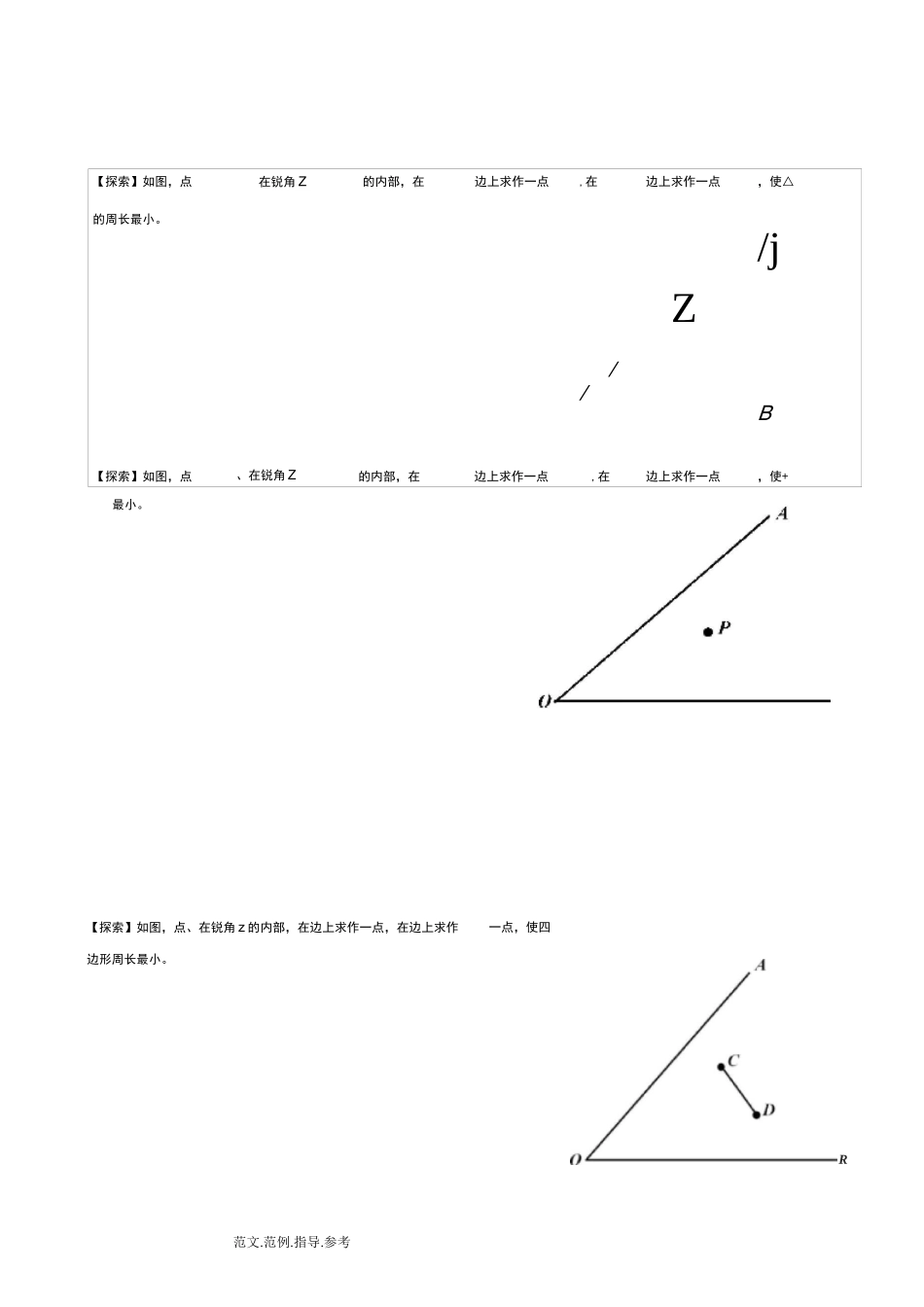
范文.范例.指导.参考【探索】如图,在关于将军饮马问题的九种变形上找一点,使+最小。【探索】如图,在上找一点,使+最小。【探索】如图,在上找一点,使一最大。【探索】如图,在上找一点,使一最大。【探索】如图,在上找一点,使一最小。范文.范例.指导.参考【探索】如图,点、在锐角z的内部,在边上求作一点,在边上求作一点,使四【探索】如图,点在锐角Z的内部,在边上求作一点,在边上求作一点,使△的周长最小。/j/Z/B【探索】如图,点、在锐角Z的内部,在边上求作一点,在边上求作一点,使+最小。边形周长最小。R范文.范例.指导.参考【探索】、与直线的位置关系如图,在直线上找到、两点,且=,在的左边,使四边形的周长最短。范文.范例.指导.参考常见问题1-怎么对称,作谁的对称?2.对称完以后和谁连接?3.所求点怎么确定?首先明白几个概念,动点=定点=对称点°动点一般就是题目中的所求点,即那个不定的点=定点即为题目中固定的点=对称的点,作图所得的点,需要连线的点=那么第一个问题,怎么对称。简单说所有题目需要作对称的点,都是题目的定点=或者说只有定点才可以去作对称的°(不确定的点作对称式没有意文的)那么作谁的对称点?首先要明确关于对称的对象肯定是一条线,而不是一个点’那么是哪一条线?一般币言都是动点所芒直线:接下来对称完以后和谁连接?一句话:和另外一个顶点相连°绝对不能和一个动点相连,明确一个概念:定点的对称点也是一个定点。例如模型二和模型三’最后所求点怎么确定?首先一定要明白,所求点最后反应在图上一定是个交点:实际就是我们斫匡直线和已知直线的交点:习题练习.如图,在等边△ABC中,AB,AD丄BC,是AC上的一点,是AD上的一点,丐A,求的最小值模拟检测.如图,已知正方形ABC边长为3,点在AB边上且B二,点,分别是边BC,C的动点(均不与顶点重合),当四边形A.的周长取最小值时,四边形A的面ZBAC=30°,若在AC、AB上各取一点,使B的值最小,则这个最小值4、如图,正方形ABC的边长为在C上,丐=,是AC上的一动点,+的最小值为5、如图所示,正方形ABC的面积为,△AB是等边三角形,点在正方形ABC内,在对角线AC、在边长为cm的正方形ABC,则厶B周长的最小值为、如图,四边形ABC是正方形,最小值;中,点为BC边的中点,点cm(结果不取近似值)AB二0,为边BC的中点为对角线AC上一动点,连接B为B上的一个动点,求C的范文.范例.指导.参考.如图,在锐角△ABC中,AB二4.V,ZBAC=45°,ZBAC的平分线交BC于点,、分别是A和AB上的动点,则B的最小值是3.如图,AABC中,AB二,。即在直线AC上求一点,使最小上有一点,使+的和最小,则这个最小值为AD上分别找一点范文.范例.指导.参考积是如图,在矩形中,已知,两点的坐标分别为(,),(,),为的中点.设点是Z平分线上的一个动点(不与点重合).()试证明:无论点运动到何处,总与相等;()当点运动到与点的距离最小时,求的坐标;()已知(,-),当点运动到何处时,△的周长最小?求出此时点的坐标和厶的周长.如图,在平面直角坐标系中,直线——分别交轴轴于,两点,点为的中点点在第二象限,且四边形为矩形动点从点出发沿线段向终点运动,过点作丄,垂足为点是点关于点的对称点,求的最小值如图在五边形使得△的周长最小时,求上+z的度数'DB逆时针旋转°得到B连接范文.范例.指导.参考如图,点A()B(,)都在双曲线=一一<上,点,分别是轴,轴上的动点,当四边形AB的周长取最小值时,求所在直线的表达式如图四边形ABC是正方形,AAB是等边三角形,为对角线B不含B点)上任意一点,将B绕点A当(AB的最小值为J+时,求正方形ABC的边长.已知点A(,),点B为直线上的动点,设B(,).()如图,若点C(,)且VV,BC丄AC,求与之间的函数关系式;()在()的条件下,是否有最大值?若有,请求出最大值;若没有,请说明理由;()如图,当点B的坐标为(,)时,在轴上另取两点,,且.线段在轴上平移,线段平移至何处时,四边形AB的周长最小?求出此时点的坐标.图1图2